| Livestock Research for Rural Development 29 (7) 2017 | Guide for preparation of papers | LRRD Newsletter | Citation of this paper |
Data comprising 6850 test-day records of 800 first parity cows calving in two herds between 1997 and 2013 from the Ethiopian Holstein Friesian cattle were used to estimate variance components and genetic parameter in a random regression animal model using Wilmink function by restricted maximum likelihood method. Residual variances were assumed to be constant across the lactation trajectory in all models. Four constants (0.05, 0.10, 0.61 and 0.065 represented as RR1, RR2, RR3 and RR4 models, respectively) of Wilmink function were compared based on statistical criteria such as residual variances, coefficient of determination and mean square error criteria. Based on these criteria, RR1 model was identified best performing model. Heritability estimates and trend were close; the minimum and maximum heritabilities were obtained at the beginning and end of lactation, respectively, and ranged from 0.11 to 0.31 in all models. Genetic and phenotypic correlations from RR1, RR2, RR3 and RR4 models between adjacent records were high and declined with the interval between the test-day records increased. Except RR3 model, the genetic correlations between early and late lactation were lower than the corresponding phenotypic correlation in all models. Thus, these models are not consistent biologically. Therefore, other types of mathematical function should be investigated to fit genetic and permanent environmental variances of test-day milk yield in Holstein Friesian cattle.
Key words: correlation, heritability, test-day model, variance component
Milk yield is the most important trait in dairy cattle. Improving the milk yield through genetic selection is therefore of great importance to increase the profitability of dairy farms. Typically, in most tropical countries the information used for genetic selection consists of lactation average based on 305-day milk yield. A genetic analysis based on 305-day does not utilize all information in the data, as it does not allow simultaneous estimation of stage of lactation effects. The use of test-day yield instead of 305-d lactation yield has become the focus of much research in dairy genetics (Gengler et al 1999; Tijani et al 1999). Test-day model describe longitudinal measurements, which change over time. Such model allows continuous change of covariance of test-day records during lactation (Pool et al 2000; de Melo et al 2007). Different sub-models have been proposed for the adjustment of covariance function in test-day models (Jensen 2001). Random regression models (RRMs) have been widely used for analysis of traits whose measures are obtained sequentially over time, such as milk production and growth traits. In the RRM, the genetic lactation curve is modeled by a random function for each animal and the underlying covariance function structure is estimated directly from the data (Meyer 1998).
Different mathematical functions have been used to model variances in test-day milk yield using random regression models. However, it is not always clear which function used to model test-day milk yield data (Bignardi et al 2011). The accuracy of estimates of genetic parameters from RRM in part depends on the covariables functions used. So far non-parametric functions have been used widely to model the random permanent environmental and additive genetic effects in test-day milk data using RRMs and the fixed lactation curves are usually modelled by parametric functions. In modelling the fixed lactation curves the most widely used function is the exponential function of Wilmink (López-Romero and Carabaño 2003; de Melo et al 2007). Wilmink function has reported to appropriately model fixed lactation curves in many studies (Lidauer et al. 2003, Negussie, et al. 2006, Meseret et al. 2015). However, so far its use in modelling random genetic and permanent environmental effects and its effect on the resulting estimates of genetic parameters are scant in scientific literature. Particularly, the use such parametric function in modeling random effects in test-day milk yield data from tropical Holstein Friesians have not been reported.
The objectives of this study were to estimate genetic parameters for test-day milk yield in tropical Holsteins and to assess the effects of Wilmink parametric function with varying exponential constants (0.05, 0.10, 0.61 and 0.065) in modelling random additive genetic and permanent environmental effects.
Data for this study was extracted from the Ethiopian national dairy cattle milk recording database. It comprised test-day milk yield records of first-lactation Holstein Friesian cows that have calved between 1997 and 2013. The data was edited for outliers and records that did not meet the edition criteria were deleted. The criteria accepted only test-day records from DIM 5 to DIM 305 and only cows with a minimum of 5 test-day records were considered. In addition, records of cows with age at calving less than 20 months or greater than 54 months were excluded. Age at calving was grouped into five classes (in months). These classes included cows less than 27, 28 to 33, 34 to 39, 40 to 45 and above 45 months of age at first calving. The calving season were divided into three distinct seasons: long dry (October - February), short rainy (March - May) and long rainy (June -September). The final dataset used included 6850 first lactation test-day milk yield records from 800 cows, which were daughters of 149 sires from two herds. The pedigree file contained 1779 animals of which 800 had own performance records. The pedigree file was pruned and prepared for analysis using the Relax2 program (Strandén 2006).
A random regression model was used for the analysis test-day milk data using the Wilmink parametric function. The Wilmink function was used to model the fixed lactation curve within calving season as well as the random permanent environment and additive genetic effects.
According to Wilmink (1987), the parameter a, b and c are associated with the level of production, the increase of production before the peak, and with subsequent decrease, respectively, and d is days in milk and parameter k is related to the time of peak lactation and usually assures a constant value. For this study comparison of various constants, 0.05, 0.10, 0.61 and 0.65, were used to model the fixed and random effects of the RRM and the models are represented as RR1, RR2, RR3 and RR4, respectively.
The RRM used for the analysis of the test-day milk yield data was described as follow:
 |
Where:
yjkilnmo is milk yield records on test-day o;
hi is herd effect;
b jr is vector with fixed regressions coefficient specific to calving season subclass j and measured on dim (d);
ɑɡk is the fixed age classes
syl is random sire*calving year interaction;
htmn is random herd test month effect;
p mr is vector with random permanent environmental effects of cow m;
ɑ mr is vector with additive genetic random regression coefficients specific to the animal effect of cow m and
ɛ ijklmo is residual effect
The variance structure for the random effects of the model was assumed that:
 |
Where: I is the identity matrix, σs2 and σh2 is the variance of the random sy and htm effect, A is the matrix of additive genetic relationships among animals, ⊗ is the Kronecker product, P and G are covariance matrices for permanent environmental and additive genetic effects, R is the diagonal matrix of the form Iσe2, and σe2 is the residual variance.
The restricted maximum likelihood using the average information algorithm was used for the estimation of variance components. The analyses were done using DMU multivariate mixed model package (Madsen and Jensen 2013). Convergence of solutions was determined when the difference between the right hand side and left hand side was less than 10-6. Genetic parameters were calculated from the resulting random regression solutions for all RRMs.
The additive genetic σ2ɑ(d) and permanent environmental σ2pe(d) variances were estimated as:

|
Where G and P = matrices of additive genetic and permanent environment random regression coefficients, respectively; ɸ= (co) variables related to a specific test-day d t measured during dim d.
Heritability for a particular DIM di in lactation was calculated by dividing the estimated genetic variance by the sum of the total phenotypic variance.
 |
Genetic correlations were calculated as the genetic covariance between diiandd djjdivided by the square root of the product of the genetic variances att diiandd djj.
Similarly, the phenotypic correlation was calculated dividing the phenotypic covariance between days di and dj, divided by the product of square root of phenotypic variances of day diandd dj .
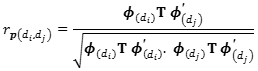 |
Where : T is the covariance matrix of the phenotypic regression coefficient
The models were compared based on the residual variance, coefficient of determination and mean square error. The analysis of residual variance is a common and simple technique in the evaluation and comparison of competing models. The models were also compared using coefficient of determination (R 2) which indicates the proportion of the variation in test-day milk yield explained by the model and mean square error (MSE) is a kind of generalized standard deviation. In this study, calving season was considered in fixed effect and explained the lactation curve. Therefore, MSE was estimated based on the actual and predicted test-day milk yield lactation curves of three calving season for each model. Lastly, the mean square error calculated for each models by taking the average of the three mean square error of three fixed lactation curves.
The overall mean test-day milk yield was 11.1 kg, with a standard deviation of 3.93 kg. Costa et al (2008) and Bignardi et al (2011) in Brazilian and Torshizi et al (2011) in Iranian Holsteins cattle reported mean phenotypic test-day milk yield of 22.5, 27.5 and 29.2 kg, respectively. An increase in milk production was observed in the early lactation and followed by a gradual decrease until the end of lactation (Table 1). Thus, the average test-day milk yield was the highest during the beginning of lactation. The trend of standard deviation for test-day milk yield across lactation was almost same. The number of observations decreased as the lactation progressed (Table 1).
|
Table 1. Days in milk (DIM), number of observation (N), means and standard deviation (SD) for milk yield in first lactation Holstein Friesian cows of Ethiopia |
|||
|
DIM |
N |
Mean |
SD |
|
5-30 |
601 |
12.9 |
3.98 |
|
31-60 |
729 |
12.9 |
3.75 |
|
61-90 |
733 |
12.1 |
3.75 |
|
91-120 |
730 |
11.5 |
3.76 |
|
121-150 |
743 |
11.0 |
3.64 |
|
151-180 |
738 |
10.7 |
3.70 |
|
181-210 |
713 |
10.3 |
3.82 |
|
211-240 |
658 |
10.0 |
3.76 |
|
241-270 |
606 |
9.8 |
3.67 |
|
271-305 |
599 |
9.3 |
3.61 |
|
All |
6850 |
11.1 |
3.93 |
The residual variances, R2 and MSE values for all models are given in Table 2. The RRM with lower residual variances and mean square error and the highest coefficient of determination were considered as better performing model. Accordingly, RR1 model could be better fit the dataset than other models. This result agree with the study of Torshizi et al (2011) who indicated that the best results obtained were from models with constant of 0.05 and 0.065. On the other hand, Silvestre et al (2006) conducted a preliminary analysis suggested 0.065 constant of Wilmink function to model test-day milk yield. In addition, based on the log-likelihood value comparison criteria, Santos et al (2013) reported that with 0.025 constant better results can be obtained.
|
Table 2. Residual variances (RV), coefficient of determination (R2) and mean square error (MSE) of random regression models for test-day milk yield in first lactation in Holstein Friesian cows of Ethiopia |
|||
|
Models |
RV |
R2 |
MSE |
|
RR1 |
2.35 |
80 |
3.03 |
|
RR2 |
2.43 |
79 |
3.52 |
|
RR3 |
2.74 |
76 |
3.39 |
|
RR4 |
2.37 |
79 |
3.59 |
The magnitudes of daily additive genetic and permanent environmental variances along the lactation trajectory are given in Figure 1 and 2, respectively. The additive genetic variances for RR1 and RR4 models showed closely similar pattern, declined from the onset of lactations at about 35 DIM and increased thereafter. The RR2 and RR3 models tended to have smaller additive genetic variance at the beginning of lactation and larger at the end of lactation. The increase in additive genetic variance with lactation progress has also been reported by Mohammadi et al (2014) in Iranian Holstein dairy cattle.
The permanent environmental variances obtained with the models were also closely similar and showed the same trend throughout lactation, except RR3 model. At the beginning of the lactation period inflated permanent environmental variances were observed for the RR1, RR2 and RR4 models. All RRMs tended to have smaller additive genetic variances and larger permanent environmental variances across the lactation trajectory. On the contrary, Santellano-Estrada et al (2008) reported larger additive genetic and smaller permanent environmental variances in RRM fitting Wilmink function. In general, the size of additive genetic and permanent environmental variances obtained in this study was higher than those reported by Santellano-Estrada et al (2008).
 |
|
Figure 1.
Additive genetic variance of RR1, RR2, RR3 and RR4 models along the lactation trajectory in Holstein Friesian cows of Ethiopia. |
 |
|
Figure 2.
Permanent environmental variance of RR1, RR2, RR3 and RR4 models along the lactation trajectory in Holstein Friesian cows of Ethiopia. |
Heritability
Most of the differences in estimated heritability among models were observed at the beginning of lactation. In general, heritability of test-day milk yield ranged from 0.11 to 0.31 across lactation (Table 3). The heritability estimates for milk yield was relatively moderate. Higher heritability estimates for daily milk yield were reported in dairy cows by Santellano-Estrada et al (2008) in the tropical lowlands of the Gulf Coast of Mexico and in southern Nicaragua and Çankaya et al (2014) in Turkey. The daily heritability estimates were was lower at the beginning and then increased until the end of the lactation. The permanent environmental variance at early stage of lactation was obtained higher and resulted lower heritability at early lactation in all the models. Biassus et al (2011) and Mohammadi et al (2014) also reported that minimum heritability of milk yield in early lactation by different functions.
|
Table 3. Estimates of daily heritabilities for RR1, RR2, RR3 and RR4 models in Holstein Friesian cows of Ethiopia |
||||
|
DIM* |
Models |
|||
|
RR1 |
RR2 |
RR3 |
RR4 |
|
|
5 |
0.17 |
0.11 |
0.19 |
0.15 |
|
35 |
0.22 |
0.23 |
0.20 |
0.23 |
|
65 |
0.24 |
0.24 |
0.21 |
0.24 |
|
95 |
0.26 |
0.25 |
0.22 |
0.25 |
|
125 |
0.27 |
0.26 |
0.23 |
0.27 |
|
155 |
0.28 |
0.27 |
0.25 |
0.28 |
|
185 |
0.29 |
0.28 |
0.26 |
0.29 |
|
215 |
0.29 |
0.29 |
0.28 |
0.29 |
|
245 |
0.29 |
0.30 |
0.29 |
0.30 |
|
275 |
0.29 |
0.30 |
0.30 |
0.30 |
|
305 |
0.29 |
0.31 |
0.31 |
0.30 |
|
* Days in Milk |
||||
The genetic and phenotypic correlations are in Figure 3 and 4, respectively. Estimates of genetic correlations between days in milk 5 and all other days were between 0.01 and 0.99, 0.12 and 0.99, 0.62 and 0.99, and -0.02 and 0.99 in RR1, RR2, RR3 and RR4 models, respectively. Genetic correlation between test-day milk yields decreased as the distance between test-days increased for all models. Higher genetic correlations between adjacent test-days milk yield has also been reported by Biassus et al (2011), Bignardi et al (2011), Çankaya et al (2014) and Mohammadi et al (2014). The phenotypic correlation ranged from 0.29 to 0.99, 0.21 to 0.99, 0.41 to 0.99 and 0.26 to 0.99 in RR1, RR2, RR3 and RR4 models, respectively. The result in Figure 4 showed that phenotypic correlations between test-days decreased as the distance between test-days increased.
The genetic correlations between early and late lactation were extremely lower in RR1, RR2 and RR4 models. Moreover, except for RR3 model, the genetic correlations between early and late lactation were lower than the corresponding phenotypic correlations. However, biologically the phenotypic correlation is lower than that of the corresponding genetic correlation and this result contrasts most studies that reported random regression models for test-day milk yield (Biassus et al 2011; Çankaya et al 2014; Mohammadi et al 2014). Therefore, except RR3 model, the genetic correlation estimates from this study, seems biologically implausible. This may be due to the inability of the Wilmink function to properly model random additive genetic variances across different stages of lactation.
 |
| Figure 3.
Estimates of genetic correlations between days in milk 5 and all other days
from RR1, RR2, RR3 and RR4 models in Holstein Friesian cows of Ethiopia. |
 |
| Figure 4.
Estimates of phenotypic correlations between days in milk 5 and all other
days from RR1, RR2, RR3 and RR4 models in Holstein Friesian cows of Ethiopia. |
The authors would like to acknowledge the Ethiopian Ministry of Agriculture, National Artificial Insemination Center for providing the data. The authors are also grateful to the Natural Resources Institute Finland, Department of Biometrical Genetics for their support in the data analyses. Addis Ababa University and Wolaita Sodo University are acknowledged for their financial support.
Biassus L D O, Cobuci J A, Costa C N, Rorato P R N, Neto J B and Cardoso L L 2011 Genetic parameters for production traits in primiparous Holstein cows estimated by random regression models. Revista Brasileira de Zootecnia 40: 85-94.
Bignardi A B., El Faro L, Torres Júnior R A A, Cardoso V L, Machado P F and Albuquerque L G 2011 Random regression models using different functions to model test-day milk yield of Brazilian Holstein cows. Genetics and Molecular Biology 10:3565-3575.
Çankaya S, Takma Ç, Abaci S H and Ülker M 2014 A Comparison of Some Random Regression Models for First Lactation Test Day Milk Yields in Jersey Cows and Estimating of Genetic Parameters. Kafkas Universitesi Veteriner Fakultesi Dergisi 20:5-10.
Costa C N, de Melo C M R, Packer I U, de Freitas A F, Teixeira N M and Cobuci J A 2008 Genetic parameters for test day milk yield of first lactation Holstein cows estimated by random regression using Legendre polynomials. Revista Brasileira de Zootecnia 37:602-608.
de Melo C M R, Packer I U, Costa C N and Machado P F 2007 Genetic parameters for test day milk yields of first lactation Holstein cows by random regression models. Animal 1:325-334.
Gengler N, Tijani A Wiggans G R and Misztal I 1999 Estimation of (co)variance function coefficients for test day yield with an expectation-maximization restricted maximum likelihood algorithm. Journal of Dairy Science 82:1849.
Jensen J 2001 Genetic evaluation of dairy cattle using test-day models. Journal of Dairy Science 84:2803-2812.
López-Romero P and Carabaño M J 2003 Comparing alternative random regression models to analyse first lactation daily milk yield data in Holstein Friesian cattle. Livestock Production Science 82:81-96.
Madsen P and Jensen J 2013 DMU A Package for Analysing Multivariate Mixed Models. Version 6, release 5.2. Center for Quantitative Genetics and Genomics Dept. of Molecular Biology and Genetics, University of Aarhus Research Centre Foulum Box 50, 8830 Tjele Denmark.
Meyer K 1998 Estimating covariance functions for longitudinal data using a random regression model. Genetics Selection Evolution 30:221-240.
Mohammadi A, Alijani S and Daghighkia H 2014 Comparison of different polynomial functions in random regression model for milk production traits of Iranian Holstein dairy cattle. Annals of Animal Science 14:55-68.
Pool M H, Janss L L G and Meuwissen T H E 2000 Genetic parameters of Legendre polynomials for first-parity lactation curves. Journal of Dairy Science 83:2640-2649.
Santellano-Estrada E, Becerril-Pérez C M, de Alba J, Chang Y M, Gianola D, Torres-Hernández G and Ramírez-Valverde R 2008 Inferring Genetic Parameters of Lactation in Tropical Milking Criollo Cattle with Random Regression Test-Day Models. Journal of Dairy Science 91:4393-4400.
Santos D J A, Peixoto M G, Borquis R R, Verneque R S, Panetto J C and Tonhati H 2013 Comparison of random regression models to estimate genetic parameters for milk production in Guzerat (Bos indicus) cows. Genetics and Molecular Biology 12:143-153.
Schaeffer L R, Jamrozik J, Kistemaker G J and Van Doormaal B J 2000 Experience with a test-day model. Journal of Dairy Science 83:1135-1144.
Silvestre A M, Petim-Batista F and Colaco J 2006 The Accuracy of Seven Mathematical Functions in Modeling Dairy Cattle Lactation Curves Based on Test-Day Records From Varying Sample Schemes. Journal of Dairy Science 89:813-1821.
Strandén I 2006 RelaX2 Version 1.10 Update 10/07. Biometrical Genetics Agrifood Research Finland. Jokioinen, Finland.
Tijani A, Wiggans G R, Van Tassell C P, Philpot J C and Gengler N 1999 Use of (co)variance functions to describe (co)variances for test day yield. Journal of Dairy Science 82:226.
Torshizi M E, Aslamenejad A A, Nassiri M R and Farhangfar H 2011 Comparison and evaluation of mathematical lactation curve functions of Iranian primiparous Holsteins. South Africa Journal of Animal Science 41:104-115.
Wilmink J B M 1987 Adjustment of test-day milk, fat and protein yields for age, season and stage of lactation. Livestock Production Science 16: 335-348.
Received 17 February 2017; Accepted 17 April 2017; Published 2 July 2017