Genetic parameters by Bayesian inference for milk yield of dual-purpose buffaloes in Colombia

Genetic parameters for test-day milk yield in Murrah buffaloes were estimated using Bayesian inference. Data comprised 81479 test-day milk records from 4886 buffaloes. The relationship matrix included 16066 buffaloes from 17 generations, with 835 inbred animals and 6.44% inbreeding coefficient. Heritabilities, repeatabilities, as well as genetic (GC), permanent environment (PeC), phenotypic (PC) and residual (RC) correlations between milk yield test day (MY) were estimated in a Colombian dual-purpose buffalo population through the Markov chain Monte Carlo methodology using a repeated measures animal model.

During lactation, MY ranged between 4.55 ± 1.4 L and 3.06 ± 1.07 L, estimated heritability values ranged from 0.10 to 0.13, and repeatabilities ranged from 0.21 to 0.25. The GC, PeC, PC and RC varied from 0.94 to 0.39; 0.94 to 0.48; 0.6 to 0.12; and 0.48 to 0, respectively. Results indicate that Colombian dual-purpose buffalo population presents genetic variation for milk yield and it is viable to conduct direct genetic improvement of this trait. Variability in milk yield of buffalo in Colombia is mainly due to the environment; therefore, genetic progress through selection of bulls with genetic merit is expected to be slow.

Introduction

The raising of Asian water buffaloes – domestic water buffalo (Bubalus bubalis) - for production of high quality milk and meat is rapidly increasingin Colombia (Agudelo et al 2007). This species is known for its adaptability to grazing systems with pastures of low nutritional value (Angulo et al 2005; Bolívar et al 2012). The main objective of dual-purpose buffalo farms in Colombia is to produce milk given its high quality and the price industry pays for milk rich in fat, protein and total solids (Bolívar et al 2014). A secondary objective is the production of calves.

This specie was introduced to Colombia in the 1960s. Unlike cattle, buffalo population has increased in recent years (Agudelo et al 2007), as well as the interest in investigating its productive characteristics. The assessment of buffalo genetic parameters is essential for estimating breeding values, to optimize selection procedures, and predict genetic progress (Bolívar et al 2010). Understanding of farm productivity is required to evaluate the effect of genetic and environmental factors influencing buffalo performance (Cerón-Muñoz et al 2012).

The estimation of genetic parameters for milk-production of buffaloes in Colombia has been approached using restricted maximum likelihood methods (Hurtado-Lugo et al 2011; Cerón-Muñoz et al 2011; Cerón-Muñoz et al 2012, Agudelo et al 2015a, Agudelo et al 2015b). However, this method includes the use of approximations, assumes asymptotic normality, provides only approximate confidence intervals for genetic parameters, and does not calculate the distribution and variance of the estimators (Resende 2002). The Bayesian inference methods can fix those problems by providing accurate probability intervals for the estimation of genetic parameters, as data can be exactly distributed a posteriori, regardless of their extension (Mendes et al 2012). When dealing with large data sets, a priori information tends to be subjugated by the probability function in establishing the a posteriori distribution, and the estimated parameters are similar to those obtained by methods based on probability functions. However, if the sample size is limited by restricted maximum likelihood, it only produces well-defined properties for large enough sample sizes (Gianola and Fernando 1986). Carneiro Júnior et al (2007) and Mendeset al (2012) reported that Bayesian methods are very suitable for the analysis of small populations when extensive historical information is available. The aim of this study was to estimate genetic parameters for milk production during the control day of dual-purpose buffaloes in Colombia using Bayesian inference.

Materials and Methods

A total of 81479 production records from 13284 lactations of 4886 buffalo cows in 16 dual-purpose dairy herds were used. These farms were included in the milk control program of the Colombian Association of Buffalo Breeders and Universidad de Antioquia, Medellin, Colombia. The relationship matrix consisted of 16066 animals from 17 generations, of which 835 were inbred individuals with 6.44% inbreeding coefficient (Figure 1).

Figure 1. Parenthood matrix by generation and inbreeding coefficient for dual-purpose buffalo systems in Colombia.

Test-day milk yields were divided into monthly lactation classes (1 to 8 classes), and contemporary groups (G) were created including farm, year, and farrowing season (December to July and August to November). To estimate variance components, heritability, repeatability and correlation, a bi-characteristic analysis using repeated measures animal models were conducted. The models included the fixed effect of G and direct random, permanent environmental, and residual effects, assuming a Gaussian distribution.

The Markov chain Monte Carlo (MCMC) method and the MCMCglmm library (Hadfield 2010) of the R-project computer program (R Core Team 2012) were used. Between 100000 and 130000 total iterations were used for each bi-trait analysis. Iterations were randomly sampled, with a discard period (burn-in) of 30000 and sampling intervals every 20 iterations.

Results and Discussion

As shown in Figure 2, average milk yield (MY) varied between 4.55 ± 1.4 L and 3.06 ± 1.07 L between the first and eighth month of lactation. Similar results were reported by Rodrigues et al (2010), using Multiple Trait Derivative Free Restricted Maximum Likelihood MTDFREML, and also by Fraga et al (2003) and Jorge et al (2005) in Murrah breed. However, these values are lower than those reported in Brazil and Italy (Breda et al 2010; Rosati and Van Vleck 2002). Differences may be due not only to the environmental conditions but also to variability of the genetic structure in Colombian herds as genetic evaluations are just beginning in Colombia, unlike countries were these assessments are conducted more regularly.

Figure 2. A posteriori distribution, means and modes for milk yield (L/day) between the first and
eighth month of lactation in buffalo cows under dual-purpose systems.

Means, medians and modes of genetic parameters for milk yield in all lactation months were similar in terms of heritability and repeatability (Figures 3 and 4, respectively), in agreement with report by Carlin and Louis (2000), expecting similar values for a posteriori marginal density that follows a normal distribution.

Figure 3. A posteriori distribution, means and modes of heritability for milk
yield between the first and eighth month of lactation in
buffalo cows under dual-purpose systems.

Figure 4. A posteriori distribution, means and modes of repeatability for milk
yield between the first and eighth month of lactation for
buffalo cows in dual-purpose systems.

The mode is the most appropriate measure for a posteriori distributions and best reflects the high frequency values, maximum distribution (Wright et al 2000). It is important to recognize that other central tendency measures, such as the mean and median, can also summarize a posteriori distributions, especially if the densities are symmetrical to each other. Any of these measures are equivalent (Mendes et al 2012; Mendes et al 2013), as is the case in this study.

The estimated heritability for MY was low to moderate (mode = 0.1 to 0.13) between the first and eighth months of lactation suggesting that this feature has a significant additive genetic variation, ie, it is a good alternative and has clear potential for genetic improvement using direct selection. Studies in buffalo using Bayesian inference reported heritability of 0.22 (Aspilcueta-Borquis et al 2010) and 0.16 (Mendes et al 2012) for Murrah and Jaffarabadi breeds, respectively. Ramos et al (2006), Tonhati et al (2008) and Rodrígues et al (2010) reported heritabilities of 0.21, 0.19 and 0.25 using REML in Murrah breed. However, Araújo et al (2008) reported higher scores (0.39) using Bayesian inference in the same breed.

In general, heritabilityies indicate significant additive genetic variation among individuals and, therefore that genetic progress can be achieved for a given trait. Low heritability values indicate that only a small part of the variation observed in the studied characteristic is attributable to additive genetic effects, suggesting that this trait is highly affected by the environment and management and feeding improvements are required to increase milk yield.

Repeatability (mode) for MY between the first and eighth months of lactation varied between 0.21 and 0.28, indicating that selection of animals based on information from early lactation could lead to erroneous MY estimates and, therefore, selection of low-producing animals. Therefore it is advisable to continue improving this trait, so, fewer records per animal will be required and the less promising females could be quickly culled. Ramos et al (2006), Rodríguez et al (2010) and Mendes et al (2012) reported repeatability coefficients of 0.32, 0.33 and 0.58 for MY, respectively.

Genetic correlations are shown in Figure 5. These correlations were higher than 0.88 between adjacent controls. The lowest genetic correlation for MY among lactation months occurred between the first and eighth controls (0.39). The same trend was reported by Kettunen et al (2000), Cobuci et al (2005) and Bignardi et al (2009). According to Crews and Franke (1998) and Facó et al (2007) correlations below 0.90 might lead to changes in classification of the animals, compromising selection and genetic progress.

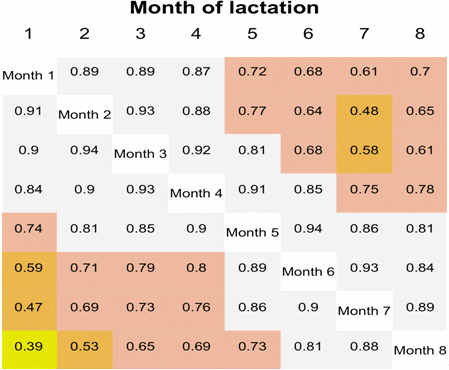Figure 5. Permanent environment correlations (above the diagonal) and genetic correlations (below the diagonal) for milk
yield between the first and eighth month of lactation in buffalo cows under dual-purpose systems.

Correlations for permanent environment (Figure 5) were medium to high, ranging from 0.94 to 0.48. The highest values occurred in consecutive months, and decreased as the controls were further apart. This suggests that both features are partially affected by the same environmental factors, which has been also reported in other studies (Araújo et al 2008; Tonhati et al 2008; Rodrigues et al 2010).

Residual and phenotypic correlations for MY between months of lactation varied between 0.0 and 0.48, and 0.12 and 0.59, respectively, being higher among consecutive months (Figure 6).

Figure 6. Residual correlations (above the diagonal) and phenotypic correlations (below the diagonal) for milk yield
between the first and eighth month of lactation in buffalo cows under dual-purpose systems.

This result indicates that this trait is not influenced by the same environmental and genetic non-additive factors over time, as evidenced by Ramos et al (2006).

Conclusion

Acknowledgements

This study was conducted by the Research Group on Animal Genetics, Breeding and Modeling (GaMMA). The Colombian Association of Buffalo Breeders (ACB) and Universidad de Antioquia (CODI Mediana Cuantía 8714-2013-5025, and CODI Sostenibilidad 2016) funded this study.

References

Angulo R A, Restrepo L F y Berdugo J A 2005 Características de calidad de las canales bufalinas y vacunas comercializadas en Medellín, Colombia. Livestock Research for Rural Development 17, Article #103. http://www.lrrd.org/lrrd17/9/angu17103.htm

Araújo C V, Cardoso A M, Ramos A A, Araújo S I, Marques J R F, Tomazini A P I e Chaves L C 2008 Heterogeneidade de variâncias e parâmetros genéticos para produção de leite em bubalinos da raça Murrah, mediante inferência Bayesiana. Revista Brasileira de Saúde e Produção Animal 9:416-425. http://revistas.ufba.br/index.php/rbspa/article/view/941/662

Aspilcueta-Borquis R R, Di Palo R, Araújo Neto F R, Baldi F, De Camargo G M F, Albuquerque L G, Zicarelli L and Tonhati H 2010 Genetic parameter estimates for buffalo milk yield, milk quality and mozzarella production and Bayesian inference analysis of their relationships. Genetics and Molecular Research 9:1636-1644. http://www.geneticsmr.com//year2010/vol9-3/pdf/gmr846.pdf

Bignardi A, El Faro L, Cardoso V L, Machado P F and Albuquerque L G 2009 Parametric correlation functions to model the structure of permanent environmental (co)variances in milk yield random regression models. Journal of Dairy Science 92:4634-4640. http://www.journalofdairyscience.org/article/S0022-0302(09)70790-8/fulltext

Bolívar D M, Ramírez-Toro E J, Agudelo-Gómez D A, Angulo-Arroyave R A y Cerón-Muñoz M F 2010 Parámetros genéticos para características reproductivas en una población de búfalos en el Magdalena Medio colombiano. Revista Facultad Nacional de Agronomía Medellín 63: 5587-5594. http://www.revistas.unal.edu.co/index.php/refame/article/view/25047/37042

Bolívar D M, Cerón-Muñoz M F, Ramírez Toro E, Agudelo Gómez D A and Cifuentes T 2012 Genetic parameters for growth traits of buffaloes (Bubalus bubalis Artiodactyla, Bovidae) in Colombia. Revista Colombiana de Ciencias Pecuarias 25:202-209. http://rccp.udea.edu.co/index.php/ojs/article/view/776

Bolívar D M, Cerón-Muñoz M F and Barahona-Rosales R 2014 Feed efficiency traits and productive performance in fifteen-month old buffaloes (Bubalus bubalis) from a dual-purpose system. Livestock Research for Rural Development 26, Article #131. http://www.lrrd.org/lrrd26/7/boli26131.html

Breda F C, Albuquerque L G, Euclydes R F, Bignardi A B, Baldi F, Torres R A, Barbosa L and Tonhati H 2010 Estimation of genetic parameters for milk yield in Murrah buffaloes by Bayesian inference. Journal of Dairy Science 93:784–791. http://www.journalofdairyscience.org/article/S0022-0302(10)71521-6/fulltext

Carneiro Júnior J M, Assis G M L, Euclydes R F, Torres R A and Lopes P S 2007 Estimation of variance components using Bayesian and frequentist inferences considering simulated data under heterogeneity of variance. Revista Brasileira de Zootecnia 36:1539-1548 supl. http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1516-35982007000700012

Carlin B P and Louis T A 2000 Bayes and empirical bayes methods for data analysis. 2.ed. London: Chapman and Hall. 440 pp

Cerón-Muñoz M F, Hurtado-Lugo N, Aspilcueta-Borquis R, Ángel-Marín P, Sepúlveda L, Albuquerque L G and Tonhati H 2011 Test-day model for milk yield of dairy buffaloes in Colombia. Livestock Research for Rural Development 23, Article #149. http://www.lrrd.org/lrrd23/7/hurt23149.htm

Cerón-Muñoz M F, Gómez-Arroyave F, Ramírez-Toro J, Cifuentes T, Gutiérrez-Molina S 2012 Parámetros genéticos para la producción de leche, grasa y proteína en búfalos de Colombia. Livestock Research for Rural Development 24, Article #030. http://www.lrrd.org/lrrd24/2/cero24030.htm

Facó O, Martins Filho R, Braga Lôbo R N, Pinheiro S M e Araújo G 2007 Heterogeneidade de (co) variância para a produção de leite nos grupos genéticos formadores da raça Girolando. Revista Ciência Agronomica 38:304-309. http://www.redalyc.org/pdf/1953/195317584012.pdf

Fraga L M, Gutiérrez M, Fernández L, Fundora O y González M E 2003 Estudio preliminar de las curvas de lactancia en búfalas mestizas de Murrah. Revista Cubanade Ciencia Agrícola 37:151-155. http://www.redalyc.org/articulo.oa?id=193018061008

Hadfield J D 2010 MCMC Methods for Multi-Response Generalized Linear Mixed Models: The MCMCglmm R Package. Journal of Statistical Software 33:1-22. http://www.jstatsoft.org/article/view/v033i02

Hurtado-Lugo N, Cerón-Muñoz M F, Aspilcueta-Borquis R, Sesana R, Albuquerque L G and Tonhati H 2011 Buffalo milk production in Brazil and Colombia: Genotype by environment interaction. Livestock Research for Rural Development 23, Article #146. http://www.lrrd.org/lrrd23/7/hurt23146.htm

Jorge A M, Andrighetto C, Strazza M R B, Correa R C, Kasburgo D G, Piccinin A, Victória C and Dominguez P F 2005 Correlation between the California Mastitis Test (CMT) and Somatic Cells Count on Milk from Murrah buffalo cows. Revista Brasileira de Zootecnia 34:2039-2045. http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1516-35982005000600029

Mendes C H, Mendes A C, Ramos A A, Souza P L, Siewerdt F and Pala A 2012 Genetic parameters by Bayesian inference for dual purpose Jaffarabadi buffaloes. Archives Animal Breeding: Archiv Tierzucht 55(6):567-576. http://arch-anim-breed.fbn-dummerstorf.de/pdf/2012/at12p567.pdf

Ramos A A, Mendes C H, Souza P L, Gonçalves H G e Machado D M 2006 Caracterização fenotípica e genética da produção de leite e do intervalo entre partos em bubalinos da raça Murrah. Pesquisa Agropecuaria Brasileira 41(8):1261-1267. http://seer.sct.embrapa.br/index.php/pab/article/view/7275/4320

Resende M D V De 2002 Genética biométrica e estatística no melhoramento de plantas perenes. Brasília: Embrapa Informação Tecnológica, 975p.

Rosati A and Van Vleck L D 2002 Estimation of genetic parameters for milk, fat, protein and mozzarella cheese production for the Italian river buffalo Bubalus bubalis population. Livestock Production Science 74(2):185 –190. http://www.livestockscience.com/article/S0301-6226(01)00293-7/pdf

Tonhati H, Cerón-Muñoz M F, De Oliveira J A, El Faro L, Ferreira A L and Albuquerque L G 2008 Test-day milk yield as a selection criterion for dairy buffaloes (Bubalus bubalis Artiodactyla, Bovidae). Genetics and Molecular Biology 31(3):674-679. http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1415-47572008000400012

Wright D R, Stern H S and Berger J 2000 Comparing traditional and Bayesian analyses of selection experiments in animal breeding. Journal of Agricultural, Biological and Environmental Statistics 5(2):240-256 http://www.jstor.org/stable/1400533?seq=1#page_scan_tab_contents

Genetic parameters by Bayesian inference for milk yield of dual-purpose buffaloes in Colombia

M F Cerón Muñoz^1,2, J P Ramírez Arias¹ and J H Agudelo Trujillo²

Abstract

Introduction

Materials and Methods

Results and Discussion

Conclusion

Acknowledgements

References

Genetic parameters by Bayesian inference for milk yield of dual-purpose buffaloes in Colombia

M F Cerón Muñoz1,2, J P Ramírez Arias1 and J H Agudelo Trujillo2

Abstract

Introduction

Materials and Methods

Results and Discussion

Conclusion

Acknowledgements

References

M F Cerón Muñoz^1,2, J P Ramírez Arias¹ and J H Agudelo Trujillo²