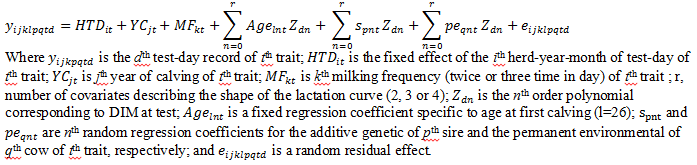Estimation of genetic parameters of milk production traits of Iranian Holstein dairy cattle using multi-trait random regression model
Mehdi Bohlouli and Sadegh Alijani
Department of Animal Science, University of Tabriz, Tabriz, Iran
M.bohluly@gmail.com
Abstract
The objective of this research was to estimate genetic
parameters of milk yield, fat yield and protein yield in Iranian Holstein
dairy cattle. A total of 868460 test day records of milk production traits
from 109574 first-parity Iranian Holstein dairy cattle were analyzed with
multi-trait random regression sire model based on Restricted Maximum
Likelihood (REML). Bivariate analyses between the production traits were
used and correlations between traits were calculated from (co)variance
components estimated in these analyses.
The heritability of milk yield, fat
yield and protein yield as a function of days in milk were estimated between
0.09 to 0.23, 0.06 to 0.12 and 0.07 to 0.23, respectively. The repeatability
for these traits ranged from 0.68 to 0.76, 0.32 to 0.59 and 0.52 to 0.67,
respectively. Genetic correlations for 305-d yield among production traits
were high, and for milk and fat, for milk and protein and for fat and
protein yields were 0.81, 0.94 and 0.86, respectively. Genetic correlations
between test-day milk and fat yields, between milk and protein yields and
between fat and protein yields at the same stage of lactation were 0.63 to
0.90, 0.84 to 0.94 and 0.66 to 92, respectively. However, Genetic
correlations were lower between milk and fat yields and between fat and
protein yields than between milk and protein yields. As relatively large
data set was used in this research, thus estimated (Co)variance components
for random regression coefficients could be used for national genetic
evaluation of dairy cattle in the Iran by random regression.
Key words: dairy cattle, genetic parameters, heritability
Introduction
Traditionally, aggregated 305-d yields have been used in dairy cows genetic
evaluation in Iran. However, the 305-d yields predicted from few
observations may give rise to bias. The use of test-day (TD) models to
analyze milk production data has several advantages over the use of models
based on 305-d yield. TD models account for environmental factors that could
affect the performance of cows throughout the lactation period. Therefore,
temporal environmental effects of individual test days can be taken into
account (Meyer et al 1989 and VanRaden 1997). Several models have been used
for estimation of (co) variance components for test-day yields.
Repeatability model assumes that the sequence of measurements of an
individual is repeated measurements of the same trait. A multi-trait model
has been applied as well (Meyer et al 1989 and Hammami et al 2008). In this
model, every test day is considered as a separate trait. Random regression
model (RRM) has been extensively used for analyzing test day yields as
suggested by Schaeffer and Dekkers (1994). In random regression models,
curves are estimated for random effects. The benefits of TD models and
analyzing TD yields by random regression methodology have been thoroughly
discussed (Swalve 2000 and Jensen 2001).
In recent years, there has been increased emphasis on estimating genetic
parameters of TD milk production traits using RRM that have been reported
for several cow populations by fitting various functions to model (Jamrozik
and Schaeffer 1997; Jakobsen et al 2002 and Hammami et al 2008). Legendre
polynomials, suggested by Kirkpatrick et al (1990) are used in many analyses
by random regression models as basic functions. The objective of this
research was to estimate (co)variance components for relatively large data
set of production traits in first parity Iranian Holsteins dairy cattle with
multi-trait random regression sire model using restricted maximum likelihood
(REML) method.
Material and methods
Data
Total of test-day records for first lactation Iranian dairy cows, between
2001 and 2010, were extracted from the Animal Breeding Center database at
Karaj, Iran. Only records of the first lactations of cows with age at first
calving between 21 and 46 month were considered in the analyses. Daily
records for milk yield, fat percentages, and protein percentages were in the
ranges 1.0 to 75 kg, 1 to 9% and 1 to 7%, respectively. Only records from
the first lactation that had data for all production traits on a given test
day were kept.
Cows were required to have a minimum of five TD records between 5 and 305
days in milk (DIM). Data edits eliminated sires that had progeny in fewer
than three herds and herds that used fewer than three sires; and also
herd-year of calving subclasses were required to have a minimum of 10 cows.
Finally, edited data set consisted of 868460 records, produced by 109574
Holstein cows with known sire (1616 bulls) in 18610 herd-year-months of
test-days (HTD). Pedigree were traced as far back as possible; therefore,
all sires have genetic relationship with these sires (recorded daughters)
kept in analysis.
Statistical models and analyses
For multi-trait analysis, the sire model fitted was as follows:
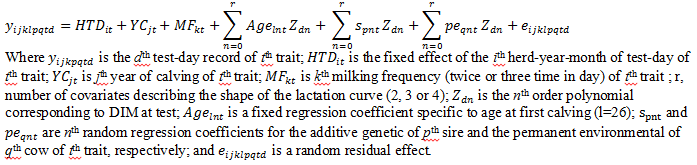


The first five polynomials were calculated from the normalized Legendre
polynomial (Kirkpatric et al 1990):



Results and discussion
Summary
statistics for the milk production traits along days in milk are shown in
Table 1. The data show an increase in milk yield in early lactation, and then
a decrease. The records were produced by 109574 Holstein
cows with known sires (Table 2) in 318 herds.
|
Table 1:
The mean and standard deviation of milk production traits in
different stage of first lactation
|
|
|
|
|
Milk (kg) |
|
Fat yield (kg) |
|
Protein yield (kg) |
|
DIM |
|
Number |
Means |
SD |
|
Means |
SD |
|
Means |
SD |
|
5-35 |
|
84720 |
28.5 |
6.83 |
|
1.03 |
0.333 |
|
0.862 |
0.222 |
|
36-65 |
|
88701 |
32.3 |
6.83 |
|
1.06 |
0.331 |
|
0.933 |
0.224 |
|
66-95 |
|
91186 |
32.6 |
6.80 |
|
1.05 |
0.323 |
|
0.955 |
0.224 |
|
96-125 |
|
92948 |
32.2 |
6.81 |
|
1.04 |
0.315 |
|
0.959 |
0.225 |
|
126-155 |
|
93554 |
31.4 |
6.94 |
|
1.03 |
0.312 |
|
0.952 |
0.228 |
|
156-185 |
|
93201 |
30.6 |
6.96 |
|
1.01 |
0.311 |
|
0.940 |
0.228 |
|
186-215 |
|
90869 |
29.8 |
6.98 |
|
1.00 |
0.311 |
|
0.925 |
0.229 |
|
216-245 |
|
87790 |
28.7 |
6.93 |
|
0.981 |
0.303 |
|
0.902 |
0.227 |
|
246-275 |
|
81022 |
27.5 |
6.92 |
|
0.964 |
0.301 |
|
0.875 |
0.228 |
|
276-305 |
|
64469 |
26.6 |
6.94 |
|
0.946 |
0.298 |
|
0.857 |
0.230 |
|
5-305 |
|
868460 |
30.2 |
7.16 |
|
1.01 |
0.317 |
|
0.919 |
0.229 |
|
Table 2:
Number of sires and daughters by class of daughters per Sire |
|
Class of number of daughters per sire |
Number of sires |
Total number of daughters |
|
5-9 |
372 |
2609 |
|
10-19 |
388 |
5417 |
|
20-49 |
376 |
11624 |
|
50-99 |
174 |
12339 |
|
100-199 |
152 |
20973 |
|
200-499 |
129 |
39597 |
|
>500 |
25 |
17015 |
|
Sum
|
1616 |
109574 |
-2log
of likelihood function (L) and Akaike information criterion (AIC) for each
of the univariate analyses for milk, fat, and protein yields are shown in
Table 3. The random regression models fitted by 2-4 orders of Legendre
polynomial (M2, M3 and M4) have been
applied to the random parts (additive genetics and permanent environmental
variances) of the sire models. Minimum of −2 ln (restricted likelihood) was
used as criterion for best fit of the applied function of the random part of
the model within trait and generally, residual variances estimated by M2 to
M4 models indicated that lowest residual variance was found for M4
model (Table 3). Therefore, The M4 models
were best for data of milk, protein and fat yields.
Cobuci et al (2005) and Costa et al (2008) reported that the Legendre
polynomials of orders 3 and 4 were the most appropriated for fitting
test-day of milk yield, by random regression model.
|
Table 3:
Analysis of goodness of fit for random regression models with
different orders of Legendre polynomial
|
|
Trait |
Model1 |
No of parameters |
-2Log(L)2 |
AIC3 |
Residual variance |
|
|
M2
|
13 |
5029474 |
5029500 |
12.2 |
|
Milk |
M3 |
21 |
4991568 |
4991610 |
11.0 |
|
|
M4 |
31 |
4971860 |
4971922 |
10.3 |
|
|
|
|
|
|
|
|
|
M2
|
13 |
88264 |
88290 |
0.0472 |
|
Fat |
M3 |
21 |
86445 |
86487 |
0.0463 |
|
|
M4 |
31 |
85572 |
85634 |
0.0454 |
|
|
|
|
|
|
|
|
|
M2
|
13 |
704925 |
704951 |
0.0162 |
|
Protein |
M3 |
21 |
702245 |
702287 |
0.0155 |
|
|
M4 |
31 |
701342 |
701404 |
0.0150 |
|
1
M2
to M4 = random regression models fitted by 2-4 orders of
Legendre polynomial for both additive genetics and permanent
environmental variances.
2
value of -2log of likelihood function (L)
3
Akaike information criterion, and AIC= -2Log (L) + 2×(number of
parameters)
|
The estimated additive genetic variances and permanent environmental and
covariances for univariate model with the smallest -2 log (L) (Table 3) are
given in Table 4; also these estimated based on multi-trait random
regression model for milk and fat yields and for milk and protein yields are
shown in Table 5 and Table 6 , respectively.
|
Table 4:
Sire additive genetic (G) and permanent environmental (P) (co)variances
for curve parameters for each traits are in the up triangle.
Correlations between curve parameters in bold are in lower off
diagonal. Residual (R) variances are shown in the bottom row. (Co)variances
for all traits are multiplied by 103 |
|
|
|
Milk yield |
|
Fat yield |
|
Protein yield |
|
G |
|
2911 |
546 |
-289 |
88.9 |
-73.6 |
|
2.33 |
0.357 |
-0.0431 |
-0.00621 |
-0.0391 |
|
2.40 |
0.605 |
-0.162 |
0.0272 |
-0.0160 |
|
|
0.553 |
336 |
-60.2 |
11.0 |
-1.12 |
|
0.398 |
0.345 |
-0.0429 |
-0.0179 |
0.00723 |
|
0.640 |
0.372 |
-0.0452 |
-0.00952 |
0.0166 |
|
|
-0.483 |
-0.297 |
123 |
-30.4 |
15.6 |
|
-0.0773 |
-0.200 |
0.133 |
-0.0553 |
0.0216 |
|
-0.385 |
-0.272 |
0.0739 |
-0.0216 |
0.00972 |
|
|
0.363 |
0.133 |
-0.605 |
20.6 |
-11.2 |
|
-0.0205 |
-0.154 |
-0.764 |
0.0394 |
-0.0198 |
|
0.119 |
-0.106 |
-0.540 |
0.0217 |
-0.0104 |
|
|
-0.408 |
-0.0183 |
0.421 |
-0.741 |
11.2 |
|
-0.193 |
0.0926 |
0.446 |
-0.750 |
0.0176 |
|
-0.104 |
0.274 |
0.359 |
-0.709 |
0.00991 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
36010 |
2742 |
-1930 |
434 |
-807 |
|
34.4 |
0.425 |
-0.973 |
-0.209 |
-0.564 |
|
28.1 |
3.03 |
-1.333 |
0.0146 |
-0.388 |
|
|
0.185 |
6113 |
-472 |
-323 |
59.8 |
|
0.0284 |
6.50 |
-1.72 |
-0.258 |
0.308 |
|
0.245 |
5.42 |
-0.407 |
-0.281 |
-0.0299 |
|
|
-0.206 |
-0.122 |
2435 |
-515 |
-164 |
|
-0.0932 |
-0.378 |
3.18 |
-1.32 |
0.0954 |
|
-0.170 |
-0.118 |
2.19 |
-0.492 |
-0.106 |
|
|
0.0696 |
-0.126 |
-0.318 |
1078 |
-379 |
|
-0.0267 |
-0.0758 |
-0.556 |
1.79 |
-0.898 |
|
0.00273 |
-0.119 |
-0.328 |
1.03 |
-0.359 |
|
|
-0.161 |
0.0289 |
-0.126 |
-0.436 |
698 |
|
-0.0857 |
0.108 |
0.0476 |
-0.598 |
1.26 |
|
-0.0905 |
-0.0159 |
-0.0888 |
-0.438 |
0.654 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
10310 |
|
45.4 |
|
15.0 |
|
Table 5: Sire additive genetic (G), Permanent
environmental (P), and residual (R) (co)variances parameters
estimated in a bivariate sire model analysis between milk yield (m)
and fat yield (f). Genetic correlations between curves parameters
are in bold. All (co)variances were multiplied by 103
|
|
|
|
m0 |
m1 |
m2 |
m3 |
m4 |
f0 |
f1 |
f2 |
f3 |
f4 |
|
G |
m0 |
2913 |
544 |
-287 |
91.2 |
-74.1 |
67.9 |
13.9 |
-0.752 |
-0.832 |
-0.842 |
|
m1 |
0.550 |
337 |
-61.5 |
8.83 |
-0.331 |
13.0 |
9.23 |
-1.01 |
-0.193 |
-0.161 |
|
m2 |
-0.484 |
-0.305 |
121 |
-30.7 |
15.2 |
-5.24 |
-1.10 |
2.61 |
-0.695 |
0.350 |
|
m3 |
0.363 |
0.103 |
-0.600 |
21.7 |
-11.4 |
2.68 |
-0.245 |
-0.376 |
0.362 |
-0.232 |
|
m4 |
-0.401 |
-0.005 |
0.404 |
-0.714 |
11.7 |
-1.78 |
0.333 |
0.102 |
-0.163 |
0.276 |
|
f0 |
0.814 |
0.457 |
-0.308 |
0.372 |
-0.336 |
2.39 |
0.352 |
-0.0652 |
0.000120 |
-0.0409 |
|
f1 |
0.435 |
0.850 |
-0.169 |
-0.0871 |
0.163 |
0.383 |
0.354 |
-0.0412 |
-0.0101 |
0.00952 |
|
f2 |
-0.0372 |
-0.147 |
0.635 |
-0.212 |
0.0778 |
-0.104 |
-0.181 |
0.143 |
-0.0510 |
0.0189 |
|
f3 |
-0.0720 |
-0.0485 |
-0.296 |
0.364 |
-0.220 |
0.000 |
-0.0801 |
-0.630 |
0.0450 |
-0.0173 |
|
f4 |
-0.110 |
-0.0621 |
0.225 |
-0.349 |
0.558 |
-0.183 |
0.120 |
0.378 |
-0.667 |
0.0164 |
|
P |
m0 |
36010 |
2724 |
-1943 |
438 |
-808 |
957 |
64.4 |
1.85 |
-20.2 |
-8.20 |
|
m1 |
0.184 |
6111 |
-472 |
-325 |
60.9 |
64.3 |
173 |
-14.8 |
-0.323 |
-2.98 |
|
m2 |
-0.207 |
-0.122 |
2438 |
-512 |
-160 |
-43.3 |
-16.2 |
65.8 |
-11.7 |
-0.768 |
|
m3 |
0.0701 |
-0.126 |
-0.316 |
1080 |
-372 |
10.9 |
-8.78 |
-14.4 |
29.1 |
-10.2 |
|
m4 |
-0.160 |
0.0295 |
-0.122 |
-0.426 |
707 |
-24.0 |
1.03 |
-4.20 |
-9.27 |
20.0 |
|
f0 |
0.852 |
0.139 |
-0.148 |
0.0564 |
-0.153 |
35.1 |
0.81 |
-0.73 |
-0.238 |
-0.582 |
|
f1 |
0.128 |
0.830 |
-0.123 |
-0.101 |
0.0153 |
0.0512 |
7.06 |
-1.44 |
-0.108 |
0.243 |
|
f2 |
0.00501 |
-0.0992 |
0.697 |
-0.229 |
-0.0832 |
-0.0651 |
-0.284 |
3.65 |
-1.09 |
0.0586 |
|
f3 |
-0.0732 |
-0.00321 |
-0.161 |
0.603 |
-0.237 |
-0.0283 |
-0.0283 |
-0.388 |
2.16 |
-0.842 |
|
f4 |
-0.0356 |
-0.0315 |
-0.0123 |
-0.249 |
0.603 |
-0.0782 |
0.0725 |
0.0254 |
-0.458 |
1.56 |
|
R |
m |
|
10310 |
|
|
|
300 |
|
|
|
|
f |
|
|
|
|
|
44.7 |
|
|
|
Table 6:
Sire additive genetic (G), Permanent environmental (P), and residual
(R) (co)variances parameters estimated in a bivariate sire model
analysis between milk yield (m) and protein yield (p). Genetic
correlations between curves parameters are in bold. All (co)variances
were multiplied by 103
|
|
|
|
m0 |
m1 |
m2 |
m3 |
m4 |
p0 |
p1 |
p2 |
p3 |
p4 |
|
G |
m0 |
3084 |
560 |
-315 |
98.5 |
-77.2 |
82.6 |
22.6 |
-5.86 |
0.0697 |
-0.163 |
|
m1 |
0.550 |
336 |
-63.4 |
11.1 |
-1.24 |
15.4 |
9.49 |
-1.06 |
0.0611 |
0.101 |
|
m2 |
-0.512 |
-0.312 |
123 |
-30.8 |
15.7 |
-8.42 |
-2.96 |
2.77 |
-0.479 |
0.103 |
|
m3 |
0.385 |
0.131 |
-0.603 |
21.2 |
-11.5 |
3.06 |
0.838 |
-0.723 |
0.431 |
-0.134 |
|
m4 |
-0.405 |
-0.0201 |
0.413 |
-0.728 |
11.8 |
-2.12 |
-0.321 |
0.387 |
-0.221 |
0.223 |
|
p0 |
0.937 |
0.528 |
-0.479 |
0.419 |
-0.389 |
2.52 |
0.604 |
-0.171 |
0.0925 |
0.000 |
|
p1 |
0.637 |
0.810 |
-0.419 |
0.286 |
-0.144 |
0.658 |
0.408 |
-0.052 |
-0.0175 |
0.0281 |
|
p2 |
-0.384 |
-0.210 |
0.910 |
-0.571 |
0.414 |
-0.395 |
-0.278 |
0.083 |
-0.0167 |
0.00925 |
|
p3 |
0.00783 |
0.0186 |
-0.273 |
0.586 |
-0.399 |
0.048 |
-0.212 |
-0.475 |
0.0312 |
-0.00680 |
|
p4 |
-0.0232 |
0.0453 |
0.0732 |
-0.227 |
0.521 |
0.00685 |
0.369 |
0.261 |
-0.681 |
0.0101 |
|
P |
m0 |
36070 |
2709 |
-1961 |
436 |
-801 |
967 |
113 |
-42.2 |
-2.93 |
-11.5 |
|
m1 |
0.182 |
6116 |
-480 |
-322 |
55.3 |
75.5 |
172 |
-11.6 |
-8.33 |
-1.43 |
|
m2 |
-0.209 |
-0.124 |
2444 |
-518 |
-159 |
-52.1 |
-10.6 |
67.7 |
-13.4 |
-5.26 |
|
m3 |
0.070 |
-0.125 |
-0.318 |
1088 |
-375 |
11.6 |
-8.12 |
-12.4 |
30.1 |
-9.28 |
|
m4 |
-0.158 |
0.0274 |
-0.120 |
-0.426 |
713 |
-22.5 |
-0.667 |
-5.56 |
-8.17 |
18.9 |
|
p0 |
0.958 |
0.182 |
-0.198 |
0.0647 |
-0.159 |
28.2 |
3.10 |
-1.31 |
-0.0312 |
-0.359 |
|
p1 |
0.253 |
0.934 |
-0.0908 |
-0.105 |
-0.0108 |
0.248 |
5.55 |
-0.385 |
-0.281 |
-0.0310 |
|
p2 |
-0.149 |
-0.0986 |
0.917 |
-0.252 |
-0.140 |
-0.165 |
-0.111 |
2.23 |
-0.469 |
-0.116 |
|
p3 |
-0.0155 |
-0.101 |
-0.258 |
0.867 |
-0.290 |
-0.00464 |
-0.113 |
-0.299 |
1.11 |
-0.338 |
|
p4 |
-0.0718 |
-0.0216 |
-0.125 |
-0.332 |
0.834 |
-0.0802 |
-0.0149 |
-0.095 |
-0.380 |
0.72 |
|
R |
m |
|
10300 |
|
|
|
310 |
|
|
|
|
p |
|
|
|
|
|
14.9 |
|
|
Heritabilities
of milk production traits as a function of DIM for single trait model are
shown in Figure 1. Clearly the estimates of heritability of TD records were
not constant throughout the lactation.
The heritability of milk yield, fat yield and protein yield as a function of
DIM were estimated between 0.09 to 0.23, 0.06 to 0.12 and 0.07 to 0.23,
respectively. The repeatability for these traits ranged from 0.68 to 0.76,
0.32 to 0.59 and 0.52 to 0.67, respectively. For milk and protein yields
there are higher heritability estimates than for fat yield based on DIM,
which are in accordance with many other similar investigations (Shadparvar
and Yazdanshenas 2005; Abdullahpour et al 2010; Hammami et al 2008 and
Bohlouli and Alijani 2012). Permanent environmental variances were higher at
the beginning of lactation for all traits; therefore, heritabilities are
lower in the beginning of lactation. These results are similar to those
observed by Cobuci et al (2011) and Biassus et al (2011) and also
repeatabilities are higher in this stage of lactation.
The small differences in heritability estimates between models with third
and fourth order of Legendre polynomials (M3 and M4)
do not indicate a preferred order of the Legendre polynomial (Cobuci et al
2011).
 |
Figure 1: Heritability (h2) for milk (m), fat (f), and
protein (p) yield as a function of days in milk (DIM)
for models with third
and fourth order Legendre polynomials (M3 and M4,
respectively). |
Genetic correlations for 305-d yield among production traits were high, and
for milk and fat, for milk and protein and for fat and protein yields were
0.81, 0.94 and 0.86, respectively (Table 7). These estimates were similar
with those obtained by Miglior et al (2009) using a
multiple-trait-multiple-lactation random regression model in Chinese
Holsteins. Larger genetic correlation for 305-d yield between milk and
protein yield than between milk and fat yield was reported also by Hammami
et al (2008), and Jakobsen et al (2002). The permanent environmental
correlations for 305-d yield between yield traits were also high. The large
permanent environmental correlations (from 0.97 to 0.99) were found among first
lactation yields (Hammami et al 2008).
|
Table 7: Estimates of heritabilities (diagonal and bold),
genetic (above diagonal) and permanent environmental (below diagonal) correlations for 305-d milk, fat, and protein yields |
|
Trait |
Milk |
Fat |
Protein |
|
Milk |
0.30 |
0.81 |
0.94 |
|
Fat |
0.85 |
0.25 |
0.86 |
|
Protein |
0.96 |
0.88 |
0.31 |
Estimated genetic and environment correlations between test-days of milk
yields, test-days of fat yields, and test-days of protein yields at
different stages of lactation are shown in Figure 2 and Figure 3. Genetic
correlations between test-day close together are close to unity, and the
genetic correlations gradually decline as the distance between test-days
increases. These figures indicate that correlations between individual
test-day are more alike for milk and protein yield than for fat yield. A
similar pattern of genetic correlations for daily milk production traits has
been reported using a comparable random regression model (Jensen et al 2001
and Jacobsen et al 2002 and Cobuci et al 2011).
Jakobsen et al (2002) reported genetic correlations estimates higher than
0.40 for first lactation test-day milk yield of Holstein dairy cattle,
therefore much higher than some estimates observed in this study. However,
lower estimates, even close to zero, were obtained for genetic correlations
between test-day milk yields in first lactation by Cobuci et al (2005) and
Biassus et al (2011).
 |
 |
|
Figure 2: Genetic (G) correlations between test-day milk
yields, test-day fat yields, and test-day protein yields at
different days in milks (DIM) for the same trait |
Figure 3: Permanent environmental (PE) correlations between test-day
milk yields, test-day fat yields, and test-day protein yields at different
days in milks (DIM) for the same trait |
Genetic correlations between test-day milk and fat yield, between milk and
protein yield and between fat and protein yield at the same stage of lactation
are shown in Figure 4. Genetic correlations between milk and fat, milk and
protein and fat and protein were 0.63 to 0.90, 0.84 to 0.94 and 0.66 to 92,
respectively. As expected, genetic correlations between traits were high.
However, genetic correlations were lower between milk and fat yields and between
fat and protein yields than between milk and protein yields (Zavadilova et al
2005).
For milk and protein, the correlations between the same DIM in the consecutive
lactations were below 0.9 at the beginning of the lactation and above 0.9 at the
end of lactation. However, for milk and fat yields, and for fat and protein
yields, the correlations were clearly lower. Similar shapes of correlation at
the same DIM were also reported by Jakobsen et al (2002) and Zavadilova et al
(2005).
 |
|
Figure 4: Genetic correlations between the same DIM of two traits
(milk-fat, milk-protein and fat-protein) |
Low heritabilities for fat yields in this study is in accordance with results in
other studies using RR models (Hammami et al 2008; Biassus et al 2011 and
Bohlouli and Alijani 2012). As found by Ravagnolo et al (2000), fat production
seems to decline more strongly than milk or protein yield as a response to heat
stress. The decline for fat yield was observed over the whole range of
temperatures, whereas for milk and protein, the yields appeared relatively
constant until about 24°C and then declined. (Hammami et al 2008)
Genetic parameters of milk yield and protein yield obtained in this study were
moderate compared with major reports on Holstein populations but were low for
fat yield. However, low heritability estimates are caused by reduced additive
genetics and increased permanent environmental and residual variances.
Generally, the resulting estimates of (co)variances, heritabilities, genetic and
permanent environmental correlations followed the general pattern reported in
other studies.
Conclusion
-
The current evaluation system in the Iran ignores the associations between milk,
fat and protein yields based on random regression model. The suggested random
regression test-day model will be restricted to a single-trait model because the
computing requirements for a multiple-trait test-day random regression model are
still enormous. Therefore, (co)variance components for regression coefficients
estimated in this research can be used in random regression test-day model for
genetic evaluation of dairy cattle in the Iran. In additional, further research
should focus on including multiple lactation data and accounting for
heterogeneity variance.
Acknowledgment
The authors thank the Animal Breeding Center of Karaj, Iran for providing the data.
References
Abdullahpour R, Moradi Shahrbabak M, Nejati-Javaremi A and Vaez
Torshizi R 2010
Genetic analysis of daily milk, fat percentage and protein
percentage of Iranian first lactation Holstein cattle. World Applied Science
10:1042-1046.
http://idosi.org/wasj/wasj10(9)/10.pdf
Biassus I O, Cobuci J A, Costa C N, Roberto P, Rorato N, Neto J B
and Cardoso L L 2011
Genetic parameters for production traits in primiparous Holstein
cows estimated by random regression.
Revista Brasileira de Zootecnia 40:85-94.
http://www.scielo.br/pdf/rbz/v40n1/v40n1a12.pdf
Bohlouli M and Alijani S 2012
Genotype by environment interaction for milk production traits in Iranian
Holstein dairy cattle using random regression model. Livestock Research for
Rural Development. Volume 24, Article #120. Retrieved September 3, 2012, from
http://www.lrrd.org/lrrd24/7/bohl24120.htm
Cobuci J A, Costa C N, Neto J B and de Freitas A F 2011
Genetic parameters for milk production by using random regression models with
different alternatives of fixed regression modeling.
Revista Brasileira de Zootecnia 40:557-567.
http://www.scielo.br/pdf/rbz/v40n3/13.pdf
Cobuci J A, Euclydes R F, Lopes P S, Costa C N, Torres R and
Pereira C S 2005
Estimation of enetic parameters for test-day milk yield in Holstein cows using a
random regression models. Genetics and Molecular Biology 28:75-83.
http://www.scielo.br/pdf/gmb/v28n1/a13v28n1.pdf
Costa C N, Melo C M R, Packer I U, De Freitas A F, Teixeira N M
and Cobuci J A 2008
Genetic parameters for test day milk yield of first lactation Holstein cows
estimated by random regression using Legendre polynomials.
Revista Brasileira de Zootecnia 37:602-608.
http://www.scielo.br/pdf/rbz/v37n4/03.pdf
Hammami H, Rekik B, Soyeurt H, Ben Gara A and Gengler N 2008
Genetic parameters for Tunisian Holsteins using a test-day random regression
model. Journal of Dairy Science 91:2118–2126.
http://download.journals.elsevierhealth.com/pdfs/journals/0022-0302/PIIS0022030208712499.pdf
Jakobsen J H, Madsen P, Jensen J, Pedersen J, Christensen L G and
Sorensen D A 2002
Genetic parameters for milk production and persistency for Danish Holsteins
estimated in random regression models using REML. journal of dairy science
85:1607–1616.
http://download.journals.elsevierhealth.com/pdfs/journals/0022-0302/PIIS0022030202742318.pdf
Jamrozik J and Schaeffer L R 1997
Estimates of genetic parameters for a test day model with random regressions for
yield traits of first lactation Holsteins. Journal of Dairy Science 80:762–770.
http://download.journals.elsevierhealth.com/pdfs/journals/0022-0302/PIIS0022030297759964.pdf
Jensen J 2001
Genetic evaluation of dairy cattle using test-day models. Journal of Dairy
Science 84:2803–2812.
http://download.journals.elsevierhealth.com/pdfs/journals/0022-0302/PIIS0022030201747364.pdf
Kirkpatric M, Lofsvold D and Bulmer M 1990
Analysis of the inheritance, selection and evolution of growth
trajectories. Genetics 124:979–993.
http://www.genetics.org/content/124/4/979
Meyer K, Graser H U and Hammond K 1989
Estimates of genetic parameters for first lactation test day
production of Australian black and white cows. Livestock Production Science
21:177–199
Miglior F, Gong W, Wang Y, Kistemaker G J, Sewalem A and Jamrozik
J 2009
Short communication: Genetic parameters of production traits in
Chinese Holsteins using a random regression test-day model. Journal of Dairy
Science 92:4697–4706.
http://download.journals.elsevierhealth.com/pdfs/journals/0022-0302/PIIS0022030209707982.pdf
Misztal I, Tsuruta S, Strabel T, Auvray B, Druet T and Lee D H
2002
BLUPF90 and related programs (BGF90). Proc. 7th World Congress
Genetics Applied Livestock Production. Montpellier, France. CD-ROM communication
28:07.
http://nce.ads.uga.edu/wiki/lib/exe/fetch.php?media=28-07.pdf
Ravagnolo O, Misztal I and Hoogenboom G 2000
Genetic component of heat stress in dairy cattle, development of heat index
function. Journal of Dairy Science 83:2120–2125.
http://download.journals.elsevierhealth.com/pdfs/journals/0022-0302/PIIS0022030200750946.pdf
Schaeffer L R and Dekkers J C M 1994
Random regressions in animal models for test-day production in dairy cattle.
Proc. 5th World Congress Genetics Applied Livestock Production
18:443–446.
Shadparvar A A and Yazdanshenas M S 2005
Genetic parameters of milk yield and milk fat percentage test day
records of Iranian Holstein cows. Asian-Australian Journal of Animal Science
18:1231-1236.
http://www.ajas.info/editor/manuscript/upload/18_191.pdf
Swalve H H 2000
Theoretical basis and computational methods for different test-day genetic
evaluation methods. Journal of Dairy Science 83:1115–1124.
http://download.journals.elsevierhealth.com/pdfs/journals/0022-0302/PIIS0022030200749770.pdf
Van Raden P M 1997
Lactation yields and accuracies computed from test day yields and (co)variances
by best prediction. Journal of Dairy Science 80:3015–3022.
http://download.journals.elsevierhealth.com/pdfs/journals/0022-0302/PIIS0022030297762684.pdf
Zavadilova L, Jamrozik J and Schaeffer
L R 2005 Genetic parameters for test-day model with random regressions
for production traits of Czech Holstein cattle. Czech Journal of Animal Science
50:142–154.
http://agriculturejournals.cz/publicFiles/52530.pdf
Received 3 September 2012; Accepted 21 October 2012; Published 6 November 2012
Go to top