Study of the factors influencing nutritional models of different feeding systems in Bakkan region, Southern Iran
Gholam Reza Badjian*, Dahlan Ismail1, Mohammad Shahwahid Othman2 and Ali Akbar Mehrabi3
*Supported by Agricultural Research and Education Organization (AREO), Ministry of Agriculture Jihad, Iran. Tel: +98 711 7203263; Fax: +98 711 7205107; P.O. Box: 71555-617 Fars Research Center for Agriculture and Natural Resources, Shiraz-Iran
badjian@farsagres.ir
1
Department of Animal Science, Faculty of
Agriculture, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia.
2
Rainforest Academy, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor,
Malaysia..
3
Faculty of Natural Resources, University of
Teheran, Karaj, Teheran, Iran
Abstract
In crop-range-livestock integrated systems, simulation models can play an important role in evaluating the interactions between the components of systems and Decision-making can be based on the outcome of the simulation. In this study two forage production sub-models and sheep/goat energy requirement models for Cropland Production System (CPS) and highland Range Production System (hRPS) in Nomadic Production System (NPS) that link together by grazing energy intake develop and livestock energy requirements are used for estimating optimum forage production. Therefore the objective of the research is to study the models of NPS and relate the physiological aspects of the energy turnover of each sub-system to real-life situations. The estimated values of energy requirements are based on the results of studying CPS with hand feeding systems and hRPS sub-systems in Bakkan and lowland Range Production System (lRPS) out of it.
The mean metabolizable energy requirement value of sheep/goat herds in CPS shows the same in comparison with hand feeding systems and increases at the time of lambing and reflects the level of body activity for grazing in hRPS and lRPS. Energy utilization models can be coupled with appropriate models of feeds and feeding systems in rangeland, cropland, and hand feeding systems and will enable the prediction of carrying capacities in any given situation under conditions similar to those in Bakkan.
Key words: Bakkan region, Feeding systems, Nutritional models, Nomadic production system, Southern Iran
Introduction
Research on traditional nomadic pastoralism so far has been focused mainly on the relationship between animal husbandry and range ecology. The main contributing factor for integrating livestock and crop production systems is the availability of herbage in rangeland that is directly grazed by animals and the availability of forage in a croplands that directly (grazing on crop residues) and indirectly (by gathering the crop residues as part of a concentrate ) provide animal feed. The growth performance of sheep and goats and their metabolizable energy voluntary intake (MEVI) in feed source systems is dynamic in nature. It is influenced by many factors such as age and physiological status of the individual sheep or goat, quantity and quality of the available feed and environment including management systems and nomads are the manager of these executive factors in nomadic sheep production system (NPS). There are some other factors that are ecological and impact on forage production in the NPS such as wet or drought years in lowland and highland ranges, and the influence of water supply on cultivation area and cropland residue. Recorded data on integrated range/cropland systems for sheep and goats usually consists of information such as the composition of the herds, numbers of animals in the herds, number of deaths, number of sales and occasionally animal weights at the time of sales. Other more detailed information is very difficult to obtain under this extensive and intensive grazing system.
Nomads represent less than two percent (1.9%) of the total population of Iran (61 million) but they control 23% of the small livestock and providers of meat, wool and dairy products (Emadi 1995). Despite the perceived environmental costs of nomadism and the poor quality of nomadic life, many government officials recognize the fact that the economic output of nomads is achieved at very little cost to the government; it just needs to be developed to more efficient levels of production. Accordingly the objective of this research is to study the NPS in the Bakkan region, Southern Iran to identify the components of two sub-systems subsequently model the subsystems. These two sub-systems are highland range production system (hRPS) and cropland production system (CPS) as energy turnover and have their own feed quality and feeding system, which can influence the feed and energy intake of the sheep and goats. The energy intake of sheep/goat measured in this study was used for the purpose of maintenance of body weight and weight gain since the MEVI for pregnancy and lactation of grazing sheep and goats was already considered in this system. System dynamics and modeling are used to study the assessment of these complex systems.
Materials and methods
Conceptual model of the NPS production system
Figure 1 shows a conceptual model of energy flows in the NPS.
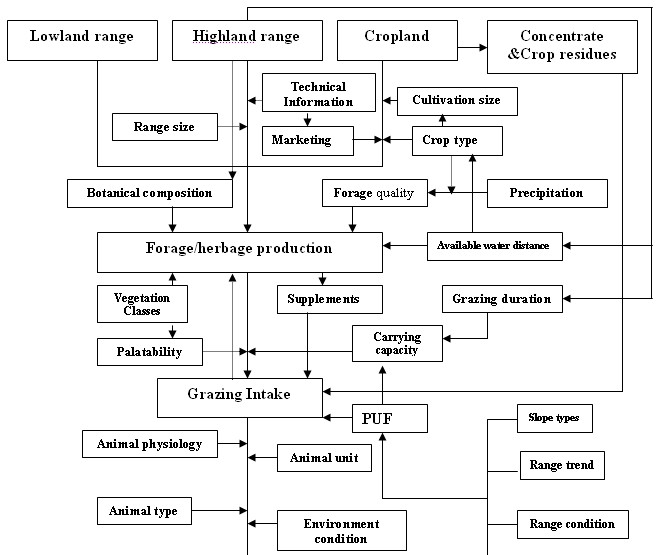  |
| Figure 1. Conceptual model of Nomadic Production System (NPS) |
Using NPS as the conceptual model, the system starts with the availability of forage in hRPS for about 3 months of the year. Each tribe of the nomads has its own grazing calendar for the hRPS during wet and drought years. The animals use lRPS, before coming to the hRPS, which is located far from the hRPS. The grazing duration in the lRPS, accompanied with supplementary feeding, is about 2.5-4 months; depending on whether it is a wet or drought year. Supplementary feed consists of barley grain, alfalfa hay, barley and bean straw that most of the nomads have gathered and carried from their cropland (during their stay in Bakkan) to the lowland. Animals start grazing on barley and bean crop residues from July to August for about 2-4.5 months. Then, conceptually the energy requirement of the grazing animals of the NPS will depend on the energy of the dry matter from hRPS, lRPS, CPS, residue and supplementary during drought and wet years. Energy flow in this conceptual model is shown in Figure 1. In an optimum situation, the grazing animal will utilize the MEVI in this system, which comes from the grazing intake (Badjian 2005). The NPS is also impacted by the environment, management system and socio/economic living of the nomads. The data in this study, such as palatability and forage index in rangeland and cropland for prediction of available forage and ME are discussed in details in PhD thesis of Badjian (2005). Furthermore some data related to animal herds such as rangeland and cropland management and their effects on forage production were obtained from a survey and deep interviews with nomads and a semi-structured questionnaire.
Conceptual model of forage production
The botanical species in hRPS can be grouped into 15 vegetation types. Conceptually, the growth of each type of vegetation or plant (production) will change according to the environment of the ecosystem (seasons) and the amount of precipitation during the year, especially in fall and winter (Badjian 2005).
Rangeland size (area) is another factor that affects the amount of forage production in the hRPS. In Bakkan, the rangeland area is negatively affected by inappropriate land management practices, e.g. overexploitation. Overstocking and extended grazing periods are current characteristics of inappropriate management practices in the study area. Rangeland trend, rangeland condition, and vegetation class have influences directly on Proper Use Factor (PUF) while the soil properties and slope properties influence PUF indirectly. PUF, and the influence of carrying capacity on PUF, have important impacts on forage availability and grazing intake based on it. Since each species of forage differs in its structure and physiological process for development and growth, the chemical constituents and energy value will vary accordingly. The growth rate of the plant and biomass production in hRPS andcultivation size in CPS is directly impacted by precipitation and water availability (Figure 1).
The available water in hRPS and CPS depends on the precipitation, also is an important factor for the water extraction from wells in CPS, and has a role for cultivated area and crop types.
Since the amount of available water to the plants comes mainly from precipitation and wells, the soil characteristics are another factor that determines the growth rate of the plants in hRPS. The amount of reserved water depends on the soil type, texture, slope, and location. Soil acts as a reservoir of water in hRPS and CPS systems. Forage production and amount of straw (residues) in CPS are related to the cultivated area, which in turn depend on the amount of precipitation and finally the available underground water (Figure 1). The straw of wheat, barley, beans, and sugar beet with alfalfa hay make up the crop residues and supplements for animal feeding during summer and winter. The qualities of the residues and supplements and grazing preferences have an impact on the grazing intake. Since the amount of precipitation differs yearly, the amount of production and the energy value of them will vary accordingly.
Livestock energy requirements model
Figure 2 shows the flow of energy requirements of sheep/goats(Badjian 2005).
 |
Figure 2. Flow of metabolism energy in the livestock in NPS |
Energy requirements of sheep/goats in NPS were divided into maintenance and production requirements. The grazing animals graze or consume the amount of energy required by their body functions if the feed availability is free choice. Breed is not specified, since it would not affect any of the calculations. The optimum productivity defines as the ratio of output over input, normalized to be equal to one in a perfect or very efficient system (Dahlan 1989).
In this study, physical output is considered, compared to the input of the system. So the live BW of animals (meat) as an output of the system is based on the availability digestible herbage/forage intake (as input of NPS). Since data on forage production and available forage under hRPS and CPS exist from field measurements and chemical analysis, and data on sheep/goat herd sizes are available from surveys, simulation studies of grazing animals will be based on the live weight dynamic changes of the herd in NPS (Badjian 2005).
In this system, the grazing animals also receive supplemental feed during winters, thus the animal energy requirements must be met solely on the available energy from the forage in the hRPS, CPS, supplemental, and crop residues.
Maintenance requirements of goats and sheep on pasture, browse, and range, especially in mountainous and transhumance (seasonal movement) grazing, are considerably higher than stable-fed animals at same physiological state because of the requirements for movement. Goats are more active and travel greater distances than sheep, which increases their energy requirements. The efficiency with which energy is utilized for weight gain, pregnancy, and lactation usually increases as the concentration of ME in the diet increases (Badjian 2005).
In Iran research activities are based upon the NRC requirements, although, researchers are currently working to establish sheep/goat requirements based on national research. Therefore, in this study two forage production sub-models and sheep/goat energy requirement models for hRPS and CPS in NPS develop.
Estimation of metabolizable energy intake models
Metabolizable energy intake models in pen-fed feeding system
The chemical analysis of 60 samples of the species in Vegetation Types (VT), cropland residues and supplementary (hand feeding) confirmed a strong relationship between Acid Detergent Fiber (ADF) and Dry Matter Digestibility (DMD). Based on it, the equation (1) shows the relationship of dry matter intake (DMI) with DMD (Badjian 2005).
DMI = 0.0537 DMD - 0.5027 (1)
Under feeding sub-system of pen-fed, the ME that the animals receive normally comes from green alfalfa hay, wheat, barley, and bean straw and in some cases top- pulp of sugar beet as roughage, and barley grain as a supplementary feed. Weaning lambs, rams and ewes in sheep flocks and does, weaning kids, and male goats in goat herds are allowed to have mixed roughage and supplementary feed such as barley grain. Therefore, the MEVI is calculated from the gross energy (GE), metabolizability (q), and voluntary feed intake (VI) as follows:
MEVI = GE * VI * q (2)
The q-value, as the fraction of digestible energy (DE) after subtraction of 19% as urine and methane, can be calculated from the following equation:
q = (1 - 0.19) * DMD or (3)
q = 0.81 * DMD (4)
Thus, with substitution of equation (4) in (2) the result can be written as:
MEVI = GE * VI * 0.81 * DMD (5)
The GE value of the pen-fed sub-system has a range from 17.33 MJ/kg DM for wheat straw to 20.13 MJ/kg DM for barley grain as a supplement. The mean GE value (18.06) is very near to the 18 MJ/kg DM reported by ARC (1980). So, the GE value of 18 MJ/kg for Dry Matter (DM) for sheep flocks is used for further calculations in this system. Thus, the equation (5) can be written as follows:
MEVI = 14.58 * VI * DMD (6)
However, it is shown that the DMD value of samples in this system ranged from 47.6 % - 85.3 %. Based on the ration, the mean DMD value of 74.2% is taken to describe the MEVI of sheep in this system. Therefore, equation (6) can be written as follows:
MEVI = 10.82 * VI (7)
For calculation of VI for sheep and goats in this system, the measured DMI is considered, based on body weight in different stages of physiological status. The MEVI value of pre-weaning lamb/goat kids (less than one year old) is measured in the MEVI value of the lactating ewe/doe. The conversion of ME into net energy (NE) is also accompanied by some loss as heat, which depends on the quality of the consumed feed and the body function for which the energy is utilized. One feature of pen-fed feeding system is that it naturally has the smallest cost for activity (energy for walking) and high value feeds due to the use of supplements. Thus, conversion of ME to NE in this system is described by the following relationship:
NERi = ki * MERi (8)
In this system, feeds are assumed ad libitum (Badjian 2005) thus; the animal will graze according to its requirements as:
MEVI = MERi or
NERi = ki * 14.58 * VI * DMD (9)
where NERi is the net energy (MJ) required for the ith body function. ki is the coefficient of the efficiency of conversion of ME to NE for the ith body function. So based on the equation (9) the VI can be expressed as;
VI = NERi / (ki * 14.58 * DMD) (10)
Thus, for the calculation of the intake required for the ith body function, the NE requirement (NERi) and the efficiency coefficient (ki) need to be specified.
Metabolizable energy grazing intake models in hRPS
The nomads use to graze their animals on the rangelands during spring. The results of a survey (Badjian 2005) show a birth rate of about 20% in spring during wet and drought years. Therefore, herds with 20% of the ewes/does in lactation are allowed to graze mixed herbage in hRPS in Bakkan. Nevertheless, the grazing intakes are determined in this study based on a sampling method. Under this system, the animals receive their required MER from six herbage groups namely: Perennial Legumes, Perennial Forbs, Shrubs, Perennial Grasses, Annual Grasses, and Perennial Grass-Likes (Badjian 2005). Therefore, the MEVI is calculated based on the GE of these herbage groups, metabolizability (q) and VI, as described in equations (2) - (6). The GE value of the species in the VT in the hRPS is 16.39 MJ/kg DM for shrubs to 17.58 MJ/kg DM for annual grass. Although the mean GE content value (16.96) is lower than the 18 MJ/kg DM reported by ARC (1980), for the calculation of MEVI of the grazing sheep in this system, the GE value of 18 MJ/kg DM is used. The DMD of the selected samples of this system has a range from 56.9% - 69.1%. So based on the mean DMD value of the species in the VT, the DMI is calculated and considered as the base for calculation of MEVI of NPS (Badjian 2005). The same estimate of MEVI is adopted for goat herds in this system. This system naturally has maximum energy cost for activity (energy for walking). Thus, conversion of ME to NE is described by the same as equations as obtained previously (8). Thus, for calculation of the intake required for the ith body function, the NE requirement (NERi) and the efficiency coefficient (ki) need to be specified (equations 9 and 10).
Metabolizable energy intake modes in CPS
The cropland is the second feeding sub-system in Bakkan. The soil and slope properties in this system will be taken as a standard for further system analysis, due to the almost uniform soil type, texture, and slope. Grazing on croplands is started after spring and during summer (most often in wet years) and summer and autumn (most often in drought years). The grazing sheep/goats are allowed to have mixed cropland residues such as barley, bean, and wheat straw, and sugar beet top pulp. Most of the nomads prefer to gather and keep them for feeding to their animals during winter as roughage in a pen-fed system. Nevertheless, the cropland residue intake was determined from the survey that was done in this study. Under this system, the ME that the animals received normally comes from wheat, barley, bean straw and top- pulp of sugar beet. Therefore, the MEVI is calculated based on the GE of these sources, metabolizability (q) and VI as is described in equations (2), (3), (4), and (5). The GE value of the cropland residue system has a range from 14.67 MJ/kg DM for barley straw to 17.8 MJ/kg DM for sugar beet tops. The mean of these GE contents (16.78) is lower than the 18 MJ/kg DM reported by ARC (1980) but for the grazing sheep, the GE value for this system is taken to be 18 MJ/kg DM. Thus, equation (4) can be used for this system too. Now, it is found that the DMD of the selected samples of this system has a range from 46.2% - 85.4%. Based on the percent of each in the ration, and a mean DMD value, the amount of DMI is estimated for NPS (Badjian 2005). The cropland residues feed production system, in comparison with the other systems, naturally has some cost for activity (energy for walking) but it has also a lower value of feeding due to the use of straws. The conversion of ME to NE is the same as that described in equations (8), (9), and (10)
Estimate of ME requirements models
ME requirements models in pen-fed feeding system
The MER of a flock sheep in a pen-fed feeding system is classified according to the need associated with body functions such as maintenance and activities, body weight gain or growth, pregnancy and lactation. The activity in this system is naturally less than in other systems, and also the value of the feeds, due to supplements (barley grain), is higher. For growing animals (lamb, wean and ram in the sheep flock and goat kid, wean, and male goat in the goat herd) the MEI is utilized for maintenance, activities and body weight (BW) gain. So the MER of a growing animal (MERgr) can be expressed as follows:
MERgr = MERm + MERg (11)
where MERm is MER for maintenance including activities and MERg is MER for live weight gain. In this study the MER is also considered for pregnant and lactating ewes and does in this system (Badjian 2005). The MEI in those stages is also considered for maintenance and activities. The following equation expresses the MER considerations for pregnant and lactating ewes;
MERmp = MERm + MERp (12)
where MERmp is the MER for maintenance and pregnancy and MERp is the MER for pregnancy.
For lactating ewes/does, the MEI is utilized for maintenance, activities, and lactation. The following equation shows this:
MERml = MERm + MERl (13)
where MERml is MER for maintenance and lactation and MERl is MER for lactation.
For a pregnant ewe/doe, nursing a lamb/kid, the MEI is utilized for both pregnancy and lactation in addition to its maintenance requirement. Thus, the MER for maintenance and pregnancy (MERmp) in the ewe can be expressed as
MERmp = MERm + MERp + MERl (14)
For the male wean and ram the MEI is utilized mainly for maintenance and activities as follows:
MERram = MERm (15)
In a pen-fed feeding sub-system, the energy cost for activities is needed more for eating, and this component should be included together with those for other activities for the daily maintenance requirements of grazing animals.
ME requirements models for maintenance in pen-fed
The amount of MERm can be expressed as:
MERm = NERm / km (16)
where NERm is the net energy requirement for maintenance (MJ/day) and km is the efficiency of utilization of ME for maintenance which can be calculated as a function of the metabolizability (q) of the consumed feed.
For this study, the km value is taken from Abbott and Maxwell (2002) as follows:
km = 0.35 * q + 0.503 (17)
Young animals have higher requirements for energy, even after scaling for metabolic live weight. This effect declines at a decreasing rate with age, an effect that can be described with an exponential function. Total NER for maintenance (NERm) are estimated based on the Abbott and Maxwell (2002) expression.
NERm = 0.26 * BW0.75 * e - 0. 0 3 A (18)
where BW is body weight (kg) and A is the age of the animal in years.
NER do not vary with metabolizability, but MER do, as inferred by the equation, defining km above. Upon substitution of equation (18) in equation (16), the MERm is expressed as follows:
MERm = (0.26 * BW0.75 * e- 0. 03 A) / km (19)
Substitution of equation (17) and (18) into equation (10) yields the feed requirements needed to meet the maintenance energy requirements as follows:
VIm = (0.26 * BW0.75 * e - 0. 03 A) / (0.35 * q + 0.503) (14.58 * DMD) (20)
where VIm is the feed required for maintenance. Based on this equation the quantity of required feed for maintenance is related to the animal's BW and feed quality.
In general, the quantity of feed required increases for heavier and younger animals and decreases with higher quality of feed, although the activities in a system such as a pen-fed system are neglected.
ME requirements models for gainin pen-fed
The MER for gain (MERg) are estimated from the following equation:
MERg = NERg / kg (21)
where NERg is the net NER for body weight gain (MJ/day) and kg is the efficiency with which ME is converted into energy for BW gain. Based on the results of the survey, sheep/goats are fed according to their requirements. So the true value of MER for gain in a pen-fed feeding system is expressed as follows:
MERg = MEI - MERm (22)
Since MERg is a ratio of the NER for gain (NERg, MJ/day) to the efficiency of utilization of ME for body gain (kg) (ARC 1980; AFRC 1990; MAFF 1987, Chaiyawan 1999), NERg can be written as:
NERg = (MEI - MERm) * kg (23)
Abbott and Maxwell (2002) showed that kg is related to metabolizability of the feed (q) as follows:
kg = 0.78 * q + 0.006 (24)
In general, NERg is dependent on the daily gain achieved and the animal's present BW. Thus the relationship suggested by MAFF (1975) is:
NERg = Dg * (6.28 + 0.0188 * BW) / (1 - 0.3 * Dg) (25)
where Dg is the daily gain (kg/day).
Hence, MERg can be expressed as a function of BW, Dg and forage quality, considering equations (22) and (23) and (24) and upon substituting equation (25) into equation (21). The daily gain of a grazing animal can be estimated based on equation (25) as:
Dg = NERg / (6.28 + 0.0188 * BW + 0.3 * NERg) (26)
On substitution of equation (19) and (23) into equation (10), the feed requirements for BW gain are obtained as follows:
VIg = [MEI - (0.26 * BW0.75 * e - 0. 03 A) / km] * kg / (kg * 14.58 DMD) (27)
In general, the quantity of feed required increases for aged and lower live BW and decreases for feed with a higher value.
ME requirements models for pregnancyin pen-fed
Total energy requirements for ewes/does in late pregnancy are seldom met by ingested feed, because physical limitations on feed intake during pregnancy makes it unlikely that ewes/does can consume sufficient feed unless it is of high quality (high metabolizability). When the deficit between the demands of the pregnancy and the supply of dietary energy is small, ewes/does can manage to meet the requirements from bodily reserves.
The MER for pregnancy can be estimated from the following equation:
MERp = NERpi / kpi (28)
where NERpi is the net energy for ith stage of pregnancy and kpi is the efficiency with which ME is converted into energy for ith stage of pregnancy.
During pregnancy ewes/does usually gained in BW due to the growth of the foetus and uterus together with the growth of the mammary gland. NER for pregnancy involve the energy deposited in the uterus and associated tissues (NERp1), the energy associated with the synthetic processes involved in foetal growth (NERp2), the energy required for foetal maintenance and the increased maternal fasting metabolism occurring during pregnancy (NERp3). Thus, total NERp as given by MAFF (1975), Konandreas and Anderson (1982), and Dahlan (1989) is defined as:
NERp = NERp1 + NERp2 + NERp3 (29)
where NERp1 = 0.03 * e (0.0174 * TC)
(30)
NERp2 = 0.452 * e (0.01 * TC)
(31)
and NERp3 = NERp2
(32)
TC is the time in days after conception which for ewes/does in Iran reaches a maximum of 151 days before birth.
The efficiency with which MERp converts into NERp depends on the different end uses of this energy. Based on the above references, the efficiency coefficients for the respective NERpi are described as follows:
kp1 = kp2 = 1.0 (33)
kp3 = km (34)
where km is the coefficient of converting MERp into NERm given by equation (16). Hence, MERp can be expressed as:
MERp = NERp1 + NERp2 + NERp3 / kp3 (35)
Substituting the values of equations (17), (30), (31), (31) and (35) into equation (10), the feed needed to meet energy requirements for pregnancy is as follows:
VIP = ((0.03 e (0.0174 * TC)) + (0.452 e (0.01 * TC))) / (0.503 + 0.35q) (14.58DMD) (36)
ME requirements models for lactationin pen-fed
The milk yield (MY) of sheep varies with breed, age, number of lambs, feed quality and availability, and stage of lactation. In Iran the (MY) of ewes/does is about 25 kg in a duration of 1.5 months for ewes and 2.5 months for does. The mean milky age of lambs and goat kids are for 101 days in Fars province based on husbandry conditions (Eilami 2000). The results of the survey in Bakkan confirm the results of Eilami (2000) so the MER for lactation can be estimated from the following equation:
MERl = NERl / kl (37)
where NERl is the net energy requirement for lactation (MJ/day) and kl is the efficiency with which MERl for lactation is converted into NERl. The kl is less than that for maintenance.
Abbott and Maxwell (2002) suggested the following relationship between kl and q:
kl = 0.35 * q + 0.420 (38)
Thus, the efficiency is related to metabolizability (q) of the feed. Based on MAFF (1975), the value of kl is about 0.60.
The net energy requirements for milk are calculated from the milk yield (MY, kg/day) multiplied by its energy content (El, MJ/kg). Hence, the NERl is approximately proportional to the quantity of produced milk:
NERl = El * MY (39)
The energy content of the milk is given approximately by the following equation (MAFF 1975), Konandreas and Anderson (1982), and Dahlan (1989):
El = 0.0386 * BF + 0.0205 * SNF - 0.236 (40)
where BF is butter fat content (g/kg), and SNF is solid-not-fat content (g/kg). For ewes and does in Iran, it is shown that BF is 60 g/kg, SNF is 13 g/kg, so the calculated energy content of milk is 2.35 g/kg, the calculated energy content of the milk of ewes is 1.03 MJ/kg and for does 0.78 MJ/kg. Substituting the values of equations (37), (38), (39) and (40) into equation (10) yields the feed requirements to produce a given quality of milk of a certain energy content.
VIl = (0.0386 * BF + 0.0205 * SNF - 0.236) MY / (0.420 + 0.35q) (14.58 DMD) (41)
The amount of milk production of ewes/does that is sold in Bakkan is not significant; it is generally used only for the lambs and goat kids. Thus, in this study The NE of ewes' milk is considered to be around 5 MJ/kg (varies with the fat content and day of lactation).
The efficiency of conversion of MEl to NEl varies from 0.6 (q = 0.52) to 0.61 (q = 0.55). The MEl required for 1kg of milk, is about 9 MJ for ewes and 5.5 MJ for does, which is close to Abbott and Maxwell's estimates (2002) which varied usually over the range from 8 to 9 MJ for ewes.
ME requirements models in hRPS and CPS
The MER of grazing sheep in hRPS and CPS are classified according to the need of body functions such as maintenance and activities, body weight gain or growth, pregnancy and lactation. The activities in these systems are naturally more than in other pen-fed sub-systems and the herbage value of hRPS is more than CPS but less than pen-fed sub-systems. For raising animals such as lambs, weans and rams in sheep flocks, weans and male goats in goat herds and productive animals such as ewes and does the MEI is utilized for maintenance, activities and BW gain. The MER for growing animals (MERgr) is the same as that expressed for the pen-fed feeding sub-system and in equations (11), (12), (13), and (14).
In hRPS, the MER was determined assuming that 20 percent of ewes and does are pregnant and lactating (Badjian 2005), plus maintenance and activities that are described in equations (12) and (13). In a situation that a ewe/doe is pregnant and nursing the lamb, the ME intake is utilized for both pregnancy and lactation in addition to its maintenance requirement. Thus, the MER of ewe/doe is similar to that expressed in equation (14).
For the male wean and ram (and male goats) the MEI is utilized mainly for maintenance and activities such as that discussed in equation (15)
In these systems, the energy cost for activities is needed more for walking and eating, and this should be included as part of the daily maintenance requirement of the grazing animals.
ME requirements models for maintenance in hRPS
In hRPS, compared to a confined system such as pen-fed feeding sub-system, grazing sheep expend additional energy for walking, climbing and, possibly, for eating. In a pen-fed feeding sub-system, the MER for maintenance (MERm) is expressed as equations (16) and (17). For relevance in situations where sheep are run at pasture, energy allowances for zero weight change must include expenditure on grazing activities and temperature regulation. Total NER for maintenance (NERm) for sheep/goats at maintenance are expressed in equation (18). Consequently, the general equation for MERm for grazing sheep, an extension of that shown on equation (20) is:
MERm = (0.26 * BW0.75 * e-0.03A) / km + 0.09 * MEI + E graze / km + E cold (42)
Generally, sheep in good grazing conditions (high stocking densities) may require an additional 20% to 40% above maintenance for grazing (E graze). In extensive grazing conditions such as in hilly country, it may increase to 50%. For adult sheep of 40 to 50 kg in thermo neutral conditions, MERm is generally in the range of 7 to 8 MJ per day, but this value can be significantly increased by low quality feed (low km), extensive grazing conditions, or cold stress (Abbott and Maxwell 2002). Due to lack of information, the energy for cold stress in Bakkan was not considered. Based on this assumption, there is a relationship between MERm, (E graze), and the percentage of steep slopes in NPS (Table 1).
|
Table 1. Relationship between steep slope (percentage) and energy for grazing (Badjian 2005) |
|
|
Steep slop or AS, % |
E graze*, % of MERm |
|
0 - 10 |
10 |
|
10 - 20 |
20 |
|
20 - 40 |
30 |
|
>40 |
40 |
|
Lowland range |
50 |
|
* E graze is energy for grazing |
|
A brief statement of the relationship can be shown in equation (43) as follows:
MERm = S MERm * %E graze * % AS (43)
where AS is the percentage of the steep slope area located in hRPS and "E graze" is the value of energy cost for activity (grazing). In this study the percentage of "E graze" is related to AS and is defined in Table 1. On consideration of equations (16), (17) and (42), the equation (10) can be rewritten to give the feed requirements needed to provide energy for maintenance:
VIm = (0.26 * BW0.75 * e - 0. 03 A) + 0.09 * MEI + E graze / km +E cold / (0.35 * q + 0.503) (14.63 * DMD) (44)
where VIm is the required feed for maintenance. Based on this equation the quantity of feed required for maintenance is related to BW, animal age, energy for walking, and feed quality.
In general, the quantity of required feed increases for heavier animals and with greater activity and decreases for feed of higher quality and for aged animals.
ME requirements models for gainin hRPS
The MER for gain (MERg) is estimated from equation (21). Based on the results of Badjian (2005), it is assumed that the sheep/goats are grazed according to their requirements. So the true values of MER, NER, kg and VIg for weight gain of the grazing sheep/goats can be expressed based on equations (22), (23), (24), (25), (26), and (27).
The NE stored per kg of live weight gain varies with the age and sex of the animal and with the rate of gain, because the proportion of fat, protein and water in the gain varies. In young animals, a lower proportion of the gain is fat and a higher proportion is protein and water than is the case for older animals.
At higher rates of gain, most of the gain is fat. The NE stored for each kg of live weight gain varies approximately from 12 MJ at 10 kg live weight, to 20 MJ in a half-grown sheep, to 26.5 MJ in a mature animal (Abbott and Maxwell 2002; APC 1990).
The efficiency of conversion of ME to NE for live weight gain varies from 0.3 for feeds of low quality (q = 0.38) to 0.51 for feeds of high quality (q = 0.65). Thus, for a half grown animal, 1kg of live weight gain will require 39 MJ ME on a high quality diet (3.25 kg of feed DM) to 53MJ ME on a low quality diet (7.5 kg of feed DM), above maintenance requirements (Abbott and Maxwell 2002). In general, the quantity of feed required for weight gains increases for aged and heavier animals, and also for higher rates of live weight gains, while decreasing for feeds of higher value.
ME requirements models for pregnancyin hRPS
The rate of energy storage in the foetus, placenta and uterus increases exponentially throughout pregnancy and, by term, the ME required to match the energy demands of a single pregnancy approaches that required for maternal maintenance alone; for a twin pregnancy, MER exceed 2 x maintenance (Abbott and Maxwell 2002).The MER for pregnancy is estimated from the equation (28). The total NERp as given by MAFF (1975), Konandreas and Anderson (1982), and Dahlan (1989) is defined in equations (29), (30), (31), and (32).
The efficiency with which MERp is converted into NERp is also defined in equations (33) and (34). Hence, the MERp is as expressed in equation (35. Equation (36) yielded the feed needed to meet the MER for pregnancy.
For a single pregnancy in a 50 kg ewe, the ME required to satisfy the energy demands of the foetus and associated maternal structures is around 5.6 MJ, on top of around 8 MJ required for ewe maintenance. In this case, the term "0.09 * MEI" is not included in calculating energy requirements for gestation (Abbott and Maxwell 2002).
ME requirements models for lactationin hRPS
The milk production of sheep varies with breed, age; number of lambs, feed quality and availability, and stage of lactation. The ME requirement for lactation can be estimated from equation (37). The kl is less than that for maintenance. Abbott and Maxwell (2002) suggested the equation (38).
ME requirements models for sheep/goat herds
The estimation of MER for sheep/goat herds was based on the traditional herd composition of nomads. The results of the survey showed that the composition for sheep flocks was 70% ewe, 13% female wean, 2% male wean, and 3% ram. The composition for goat herds was 70% doe, 12% female wean, and 5% male goat (Badjian 2005). In this study, the MEVI and MER of 12% of male and female lambs and 13% of male and female goat kids were considered as included in the feed of respectively the ewes and does in the herd. Generally, the proportion of components in a mixed herd was 40% goats and 60% sheep. The physiological status based on the nomads' management lets the herd have a continuous mating system with a fixed ram and lamb replacement rate for sheep, and a male and goat's kid birth rate needed to maintain the goat herd. The equations (45) and (46) show the relationship between the herd composition and MER achieved for ewes/does in different physiological statuses, ram/male goat, and weans:
MER of sheep herd = mean (MERm + MERg + MERl) of ewe * 0.70 + mean MERtr * 0.03 + mean MERtmw * 0.02 * MERtfw * 0.13 (45)
And MER of goat herd = mean (MERm + MERg + MERl) of doe * 0.70 + mean MERtmg * 0.05 + MERtfw * 0.12 (46)
where MERtr is the total MER for rams, MERtmg is the total MER for male goats, MERtmw and MERtfw are the total MER for male and female weans.
Results and discussion
ME requirements of grazing sheep/goat herds
The estimated values of ME for maintenance and production are based on the results of studying four feeding sub-systems in/out of Bakkan. Measurements of MER of grazing animals in these systems are complicated and difficult due to the impacts of different factors on MER. Therefore, the results of this study should be compared with studies from one or more countries with feeds and feeding systems similar to those used by producers such as nomads in Iran (Bakkan). Comparison of the results of this study with the recent findings in other countries (even in Middle East) with different condition and animal breeds showed high variations in MER of sheep/goats. However, estimated MER values of the study showed quite reasonable results when compared with other reported works such as Ebrahimi (1998). Since the predicted MER for maintenance and reproduction of sheep flocks showed some agreement with other reported values, the models of energy utilization can be adopted in order to quantify the MER of the grazing herd for maintenance and production. Table 2 demonstrates the predicted mean MER value of sheep/goat herds in four feeding sub-systems. By specifying the initial body weight, activities and physiological status, the MER of the grazing herd can be predicted according to the energy utilization models. Body weight (BW) and activities such as walking and eating are the most important factors governing the energy consumption that is included in MER for maintenance (MERm). Thus, for rams/male goats (big sizes) the MERm is higher than for ewes/does.
|
Table 2. Metabolizable energy requirement (MER) of sheep/goat herd in feeding systems (Badjian 2005) |
||||
|
Feeding sub-systems |
mean MER value of sheep herd, MJ/day |
mean MER value of goat herd, MJ/day |
||
|
Drought years |
Wet years |
Drought years |
Wet years |
|
|
Highland range |
12.4 |
12.2 |
10.9 |
11.1 |
|
Cropland residues |
11 |
11.7 |
10 |
10.3 |
|
Hand feeding |
11 |
11.2 |
11 |
10.6 |
|
Lowland range |
5.5 |
13.8 |
1.9 |
12 |
The animal husbandry of nomads is recognized to rely on the Lori breed of sheep, a normal breed (size) with mean BW of 50 kg and the Torki breed of goat with mean BW of 40 kg (0.8 of sheep breed). For smaller breed types, the carrying capacity per unit of area (hectare) will be higher and the MER per animal will be lower when compared with the bigger breed types of sheep/goat.
Since MERm represents a major portion of the energy required for animal production, the MERm of these specific breeds of animal must be considered in the process of decision making for mixed sheep/goat herds in a grazing system enterprise. The predicted mean of MER for ewes/does in different conditions of the physiological cycle, ram/male goat, and weans can be consider for a mixed sheep/goat herd. One animal unit (AU) in this study is assumed to be equivalent to one sheep with 50 kg body weight, or 0.8 AU to represent a goat of 40 kg weight. Thus, calculations of MER per AU in a sheep/goat herd will depend on factors such as sex, live body weight, feed values, grazing period, and energy cost for walking during wet or drought years. On consideration of herd composition, the mean MER value for a herd can be calculated.
Generally, the mean MER value of sheep/goats herd in lRPS is higher than in other systems during wet years. This result shows that the percentage of energy consumption that is needed for walking in this system is more during wet years but less during drought years. The results also indicate that the mean values of MER of sheep/goat herds in hand feeding systems is the same for both wet and drought years. The mean value of MER of sheep/goat herds in cropland residues is shown to be the same in comparison with hand feeding systems. This is due to the lower feed values and energy required for walking. The mean MER value of the herds in hRPS is the highest during drought years. It means that the nomads stay more in hRPS during the drought years. The mean MER values increase at the time of lambing and also reflect the level of body activity for grazing.
Acknowledgments
This paper has been released from the PhD thesis of the Senior Author: "Impact of Nomadic settlement on the ecology of Rangeland and Livestock in the Bakkan region of Southern Iran", Universiti Putra Malaysia (UPM), 2001-2005
The senor author acknowledges the support from the Agricultural Research and Education Organization (AREO), Ministry of Agriculture Jihad, Iran.
The authors are sincerely grateful to the director and technical staff of the Research Center for Agriculture and Natural Resources of Fars Province for their kind support and for provision of the research facilities.
References
Abbott K A and Maxwell W M C 2002 Sheep Health and
Production. University of Sydney.
http://vein.library.usyd.edu.au/sheephealth/index.html
Accessed on 03 May 2004.
AFRC (Agricultural and Food Research Council ) 1990 Nutritive Requirement of Ruminant Animals: Energy. Nutrition Abstracts and Reviews (series B) 60 (10): 779-804.
ARC (Agricultural Research Council) 1980 The nutrient requirement of ruminant livestock. C.A.B., Slough, England.
APC (Animal Production Committee) 1990 Feeding standards for Australian livestock, Ruminants ed JL Corbett, Standing Committee on Agriculture, Animal Production Committee, Ruminants Subcommittee, CSIRO Publications, East Melbourne, Australia.
Badjian Gh R 2005 Impact of Nomadic settlement on the ecology of Rangeland and Livestock in the Bakkan region of Southern Iran. Ph.D. Thesis, Universiti Putra Malaysia, Malaysia.
Chaiyawan Wattanachant 1999 System approach to evaluation growth and meat production of sheep under two production systems, Ph.D. Thesis, Universiti Putra Malaysia. pp: 33.
Dahlan I 1989 Modeling and simulation of Herbage and Cattle Production Systems Under Oil Palm Plantations in Malaysia, Ph.D. Thesis, Kyoto University, Japan.
Ebrahimi A A 1998 Establishment a suitable model of estimating short-term Grazing Capacity-using geographic Information System (GIS), Master of Science Thesis, Tarbiat Modaress University. Iran. pp 170. (In Persian Language)
Eilami B 2000 Study of husbandry situation (sheep and goats) in Fars Province. Final research report. Fars research center for natural resources and animal affairs. Iran (in Persian Language).
Emadi M H 1995 Pastoralists, Participation and Policy: an action oriented, systemic and participatory approach to improve the relationships between Pastoralist Nomads, government and natural resources in Iran, Ph.D. Thesis, University of Western Sydney, Hawkesbury, Australia pp 354. http://library.uws.edu.au/adt-NUWS/public/adt-NUWS20031201.102541/index.html
Konandreas P A and Anderson F M 1982 Cattle herd dynamics: an integer and stochastic model for evaluating production alternatives. ILCA Research Report no.2 International Livestock Center for Africa pp 95. http://www.fao.org/Wairdocs/ILRI/x5521E/x5521e00.htm
MAFF (Ministry of Agriculture, Fisheries, and Food) 1975 Energy allowance and feeding systems for ruminants. Technical bull. no.33.pp 79.
MAFF (Ministry of Agriculture, Fisheries, and Food) 1987 Energy allowances and feeding systems for ruminants. Reference Bulletin no.33. London, UK. : Her Majesty's Stationary Office.